Part 2

greg mc

May 2021

Contents

  • Character variety
  • Norms and counting
  • Proof of Aigner
  • Proof by snakes
  • More lengths

Character variety

H. Cohn, Approach to Markov’s Minimal Forms Through Modular Functions (1955)

  • modular torus = quotient of upper half plane \(\mathbb{H}\) by \(\Gamma\) = commutator subgroup of \(PSL(2,\mathbb{Z})\), acting by Mobius transformations
  • relates Markoff numbers to lengths of simple closed geodesics

Back to the Torus

  • \(\mathbb{Z}^2\) acting on \(\mathbb{R}^2\) by translation
  • quotient space (orbit space) is a euclidean torus
  • primitive elements \((p,q)\in \mathbb{Z}^2\)
  • \(\rightarrow\) closed curve on torus = \((p,q)\) curve
  • (usual) length \(=\|(p,q)\| = \sqrt{p^2 + q^2}\)

Usual Torus

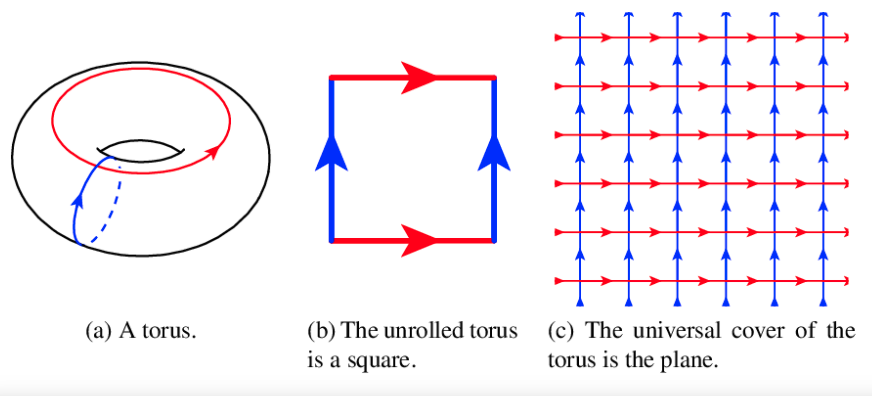
Torus

  • \(\mathbb{Z}^2\) acts by translation in lots of different ways
  • translation lengths of \((1,0),(0,1),(1,-1)\) determine (up to conjugation)
  • the representation \(\mathbb{Z}^2 \rightarrow \text{isom}(\mathbb{R}^2)\)
  • length of \((p,q)\) curve given by quadratic form

representation \(\mathbb{Z}^2 \rightarrow \text{isom}(\mathbb{R}^2)\)

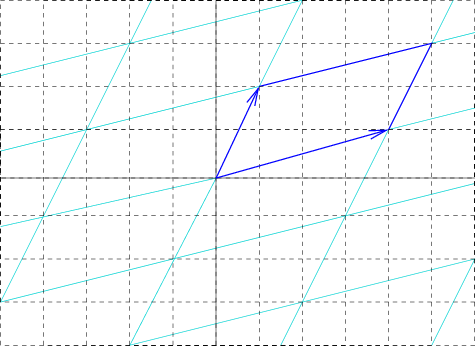
representation \(\mathbb{Z}^2 \rightarrow \text{isom}(\mathbb{R}^2)\)

Threes, triangles, tori

  • 3 side lengths determine a triangle
  • need 3 numbers to build a euclidean torus
  • what about the 3 Markoff numbers ?
  • can build a hyperbolic punctured torus
  • no simple formula for length of \((p,q)\) curve

  • modular torus = quotient of upper half plane \(\mathbb{H}\) by \(\Gamma\) = commutator subgroup of \(\text{PSL}(2, \mathbb{Z})\), acting by Mobius transformations
  • hyperbolic torus = quotient of upper half plane \(\mathbb{H}\) by \(\Gamma = \rho(\mathbb{Z}*\mathbb{Z})\),
  • \(\rho:\mathbb{Z}*\mathbb{Z}\rightarrow\text{PSL}(2, \mathbb{R})\) discrete faithful

Flat torus

Punctured torus

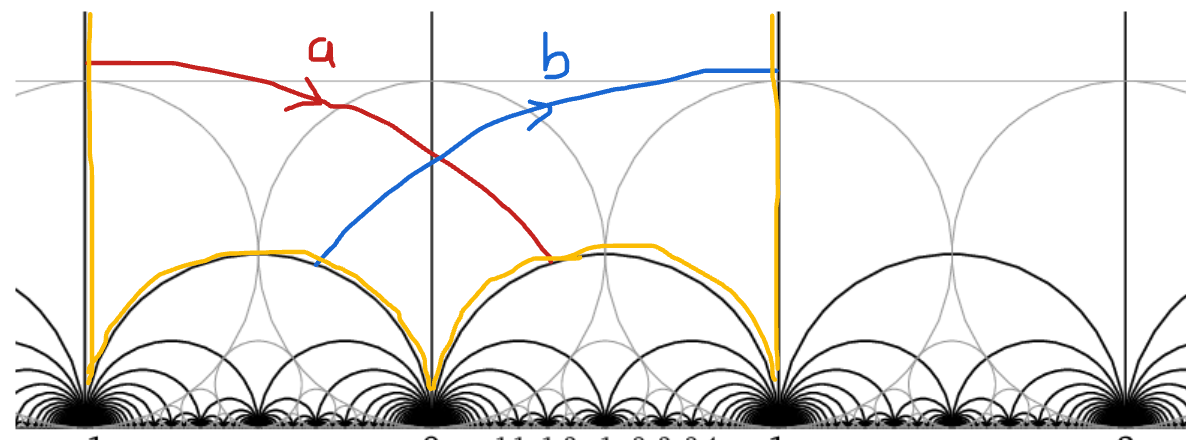
Geometry of the Markoff numbers

\(\rho:\mathbb{Z}*\mathbb{Z}\rightarrow\text{PSL}(2, \mathbb{R})\)

  • lifts to \(\hat{\rho}:\mathbb{Z}*\mathbb{Z}\rightarrow\text{SL}(2, \mathbb{R})\)
  • character map \(\chi : \rho \mapsto ( tr \hat{\rho}(a), tr \hat{\rho}(b), tr \hat{\rho}(ab) )\)
  • \(a,b\) generators of the free group = fundamental group of the torus.

Traces behave "like squares of translation lengths"

  • parallogram law
  • \(b\in SL(2,\mathbb{C}),\,b^2 - (tr b)b + I_2 = 0\)
  • (Cayley-Hamilton) \(\Rightarrow\)
  • \(tr ab + tr ab^{-1} = (tr a) (tr b)\)

Markoff cubic from the puncture

Loop round the puncture \(aba^{-1}b^{-1}\)

  • isn't trivial but it's special (parabolic)
  • corresponding matrix something like
  • \(\begin{pmatrix} \pm 1 & 6 \\ 0 & \pm 1 \end{pmatrix}\)

puncture condition

\(tr \hat{\rho} (aba^{-1}b^{-1}) = -2\)

  • \((x,y,z) = ( tr \hat{\rho}(a), tr \hat{\rho}(b), tr \hat{\rho}(ab) )\)
  • \(x^2 + y^2 + z^2 - x y z = 2 + tr \hat{\rho} (aba^{-1}b^{-1})=0.\)
  • = Markoff cubic up to a change of variable

"inverse" character map

Section: character variety to representation variety

\(\begin{pmatrix} x & -1 \\ 1 & 0 \end{pmatrix}\) \(\begin{pmatrix} 0 & \eta \\ -\eta^{-1} & y \end{pmatrix}\)

\(z = \text{trace of product} = \eta + \eta^{-1}\)

Cohn shows that the permutations and the Vieta flips used to construct Markov's binary tree are induced by automorphisms of the fundamental group of the torus.

Exo

  • Nielsen move \((a,b,ab) \mapsto (a, b^{-1}, ab^{-1})\)
  • \(tr ab + tr ab^{-1} = (tr a) (tr b)\)

Counting problem

\(N(t) =\) number of Markoff numbers \(\leq t\)

Counting closed simple geodesics

  • character map \(\chi : \rho \mapsto ( tr \hat{\rho}(a), tr \hat{\rho}(b), tr \hat{\rho}(ab) )\)
  • \(a,b\) generators fundamental group of the torus.
  • \(a\) generator iff \(\exists\) essential simple closed curves representing its conjugacy class

Simple representatives

Simple representatives in homology

\(\phi : \mathbb{Z}*\mathbb{Z} \rightarrow \mathbb{Z}^2 \simeq H^1(T,\mathbb{Z})\) abelianizing homomorphism.

  • generators \(\in \mathbb{Z}*\mathbb{Z}\) \(\mapsto\) primitive \(\in \mathbb{Z}^2\).
  • \((p,q) \in \mathbb{Z}^2\) primitive \(\Leftrightarrow p,q\) coprime.

La norme

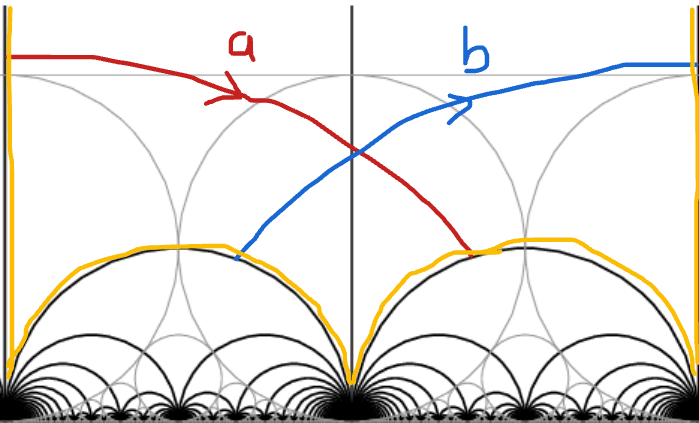
Let \(c\) be an essential closed curve \(\ell_c\) its length.

\(\gamma \in H^1(T,\mathbb{Z}), \, \| \gamma \| := \inf_{ c \in \gamma} \ell_c/2\)

  • convexity/triangle inequality
  • any pair of curves in linearly independent homology classes intersect
  • a curve with self intersections is never a minimizer

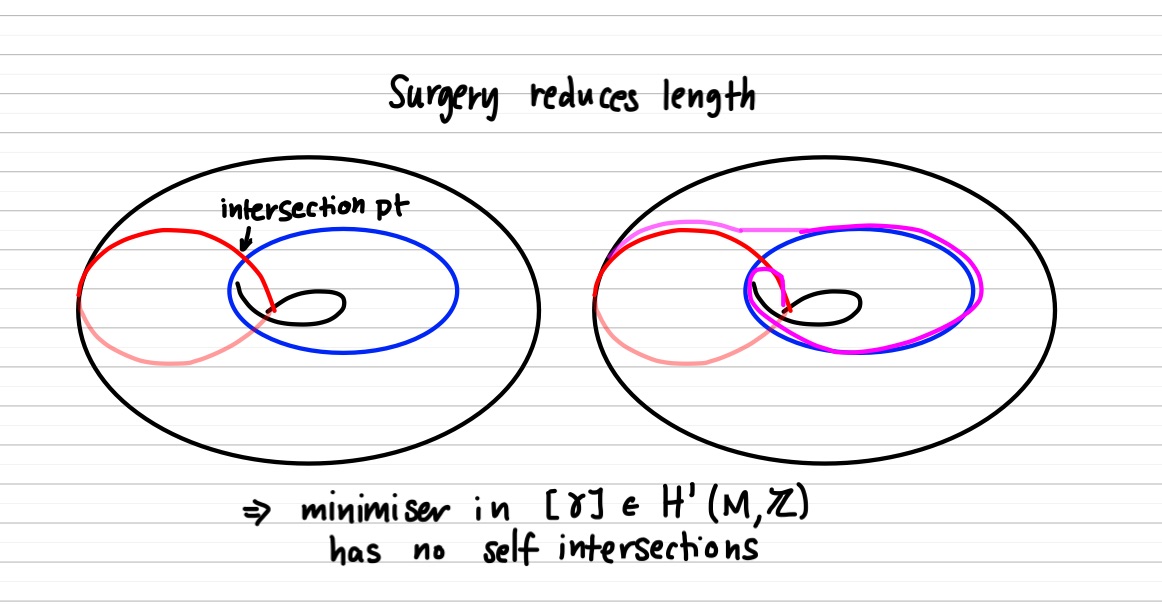
more formally from our paper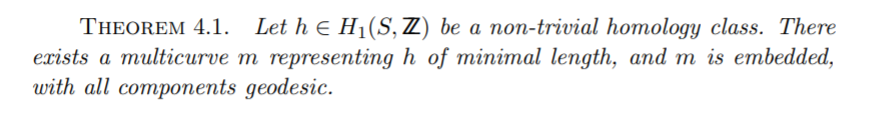

Unit ball

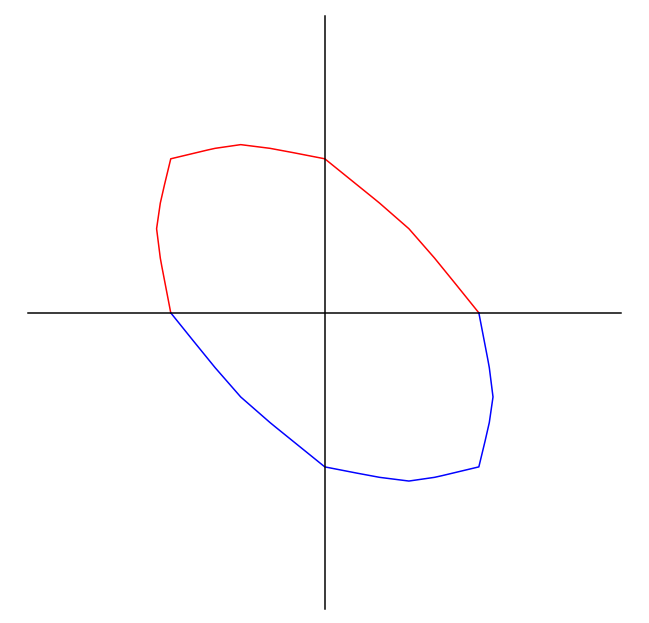
Corollary

The length function does not coincide with any reasonable function

  • not differentiable at rational slopes
  • is well approximated by piecewise linear

Unit ball and counting

  • \(\sharp \{ \gamma,\, \| \gamma \| \leq t \} \sim \text{area unit ball}\times t^2\)
  • \(\sharp \{ \gamma \text{ primitive},\, \| \gamma \| \leq t \} \sim \frac{6}{\pi^2}\text{area unit ball}\times t^2\)
  • the area of the unit ball depends on the hyperbolic structure
  • with Rivin we studied it, but now it's called the Mirzakhani function :(
  • \(\frac{6}{\pi^2}\) = proba 2 random integers coprime

Why log ?

\(N(t) = C (\log 3 ))^2 + O(\log t)\)

  • \(m_{p/q} = \frac13 tr \hat{\rho}( \gamma_{p/q})\)
  • \(= \frac23 \cosh\left(\frac{\ell_{\gamma_p}}{2} \right)\)
  • \(= \frac23 \cosh(\| (q,p) \|_s)\)

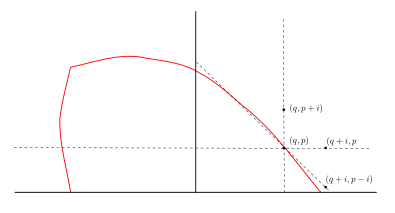
Aigner's conjectures

Aigner's conjectures

Let \(p, q\) be real non negative numbers and \(i > 0\) then

  • \(\|(q,p) \|_s < \|(q + i,p) \|_s\)
  • \(\|(q,p) \|_s < \|(q ,p +i ) \|_s\)
  • If in addition \(p < q\) then \(\|(q ,p ) \|_s < \|(q + i ,p -i ) \|_s\)

Aigners conjectures proof

source

Pair of pants

  • coprime \((p,q) \mapsto w_{p,q} \in \langle a,b \rangle\)
  • extend length from \(\mathbb{Z}^2\) to \(\mathbb{R}^2\)
  • technically, can be done in general using immersed train tracks

Goldman integer pts, orbifolds

\(x^2 + y^2 + z^2 - x y z = 20.\)

  • different \(GL(2,\mathbb{Z})\) orbts
  • (2,2,-2) three punctured sphere
  • (0,3,1) orbifold, disc with 2 cone points
  • (0, 4,2) orbifold, punctured disc one cone point

Three punctured sphere

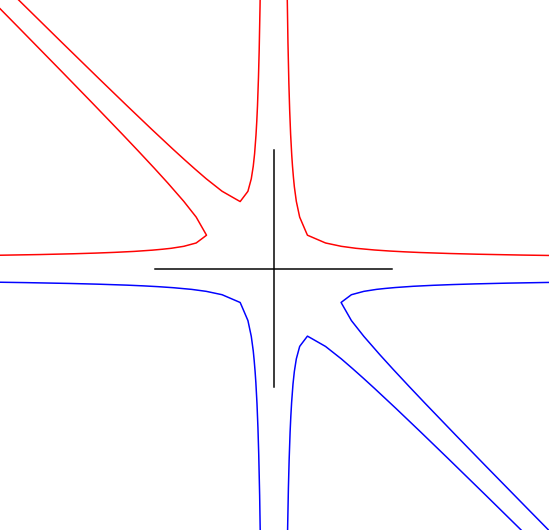
Pair of pants

\(x^2 + y^2 + z^2 - x y z \geq 20.\)

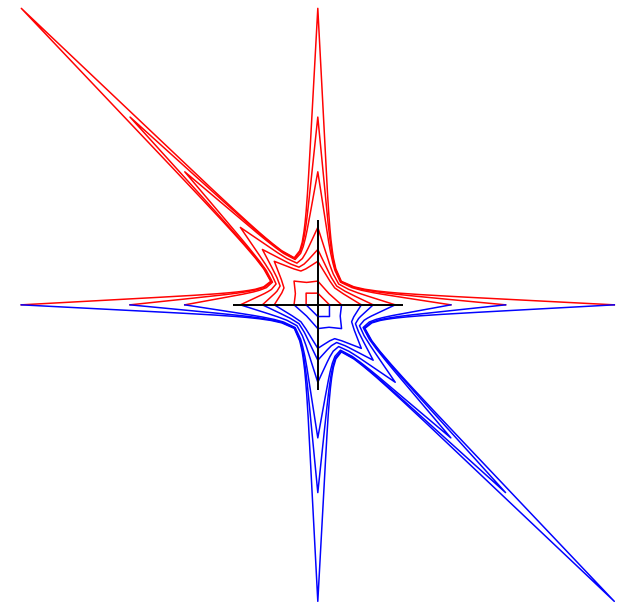
(0,4,2) orbifold

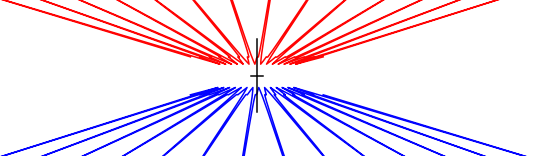
(0,3,1) orbifold

Thanks