Surface automorphisms and elementary number theory

greg mc shane

• elementary number theory (Fermat, Markoff, Button)
• hyperbolic geometry (Farey, Ford, Penner)
• try not to talk about continued fractions

• some is joint work with V. Sergiescu
• two index 6 subgroups
• three punctured sphere, automorphisms
• modular torus, automorphisms

Problem 0

Problem 1

Markoff numbers are integers that appear a Markoff triple

which are solutions of a Diophantine equation
the so-called Markoff cubic

Odd index Fibonacci numbers are Markoff numbers

Odd index Fibonacci numbers are sums of squares

Frobenius uniqueness conjecture

The largest integer in a triple determines the two other numbers.

• Only partial results
• m = Markoff number = z > y > x

• Jack Button for m prime
• Zhang An elementary proof...
• Lang, Tan A simple proof....
• Baragar m, 3m - 2, 3m + 2 prime

Problem 2:

Give a geometric proof of

If an odd prime and 4 divides then
for coprime integers .

References etc

• First proof Euler (reciprocity, descent)
• Heath-Brown, Fermat’s two squares theorem. Invariant (1984)
• Zagier, A one-sentence proof that every prime p = 1 (mod 4) is a sum of two squares, 1990
• Dolan, S., A very simple proof of the two-squares theorem, Math Gaz, 106(564). (2021) text
• Elsholtz, Combinatorial Approach to Sums of Two Squares and Related Problems. (2010)

Zagier: one sentence

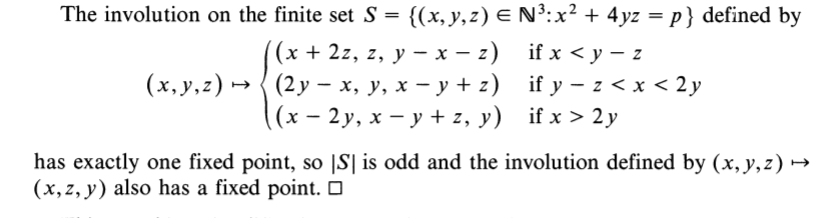
Reciprocal arcs

• modular torus = quotient of by
• pair of ideal triangles glued up
• elliptic involution swaps triangles fixes midpoint of diagonal arc
• swaps opposite edges and leaves diagonals invariant
• Def reciprocal arc = arc invariant by ell. inv.

and this

Problem 3:

Martin Aigner

• Proofs from THE BOOK
• 100 years of uniqueness
• Convexity and Aigner's Conjectures

There is a natural map (we'll see why shortly)

Aigner's monotonicity conjectures

• M. Rabideaua, R. Schiffler, Continued fractions and orderings on the Markov numbers, Advances in Mathematics Vol 370, 2020. arxiv 1801.07155
• C Lagisquet and E. Pelantová and S. Tavenas and L. Vuillon, On the Markov numbers: fixed numerator, denominator, and sum conjectures. Advances in Applied Mathematics Volume 130, September 2021 arxiv 2010.10335
• Kyungyong Lee, Li Li, Michelle Rabideau, Ralf Schiffler, On the ordering of the Markov numbers arxiv 2010.13010

Aigner's conjectures proof

Sketch of proof

Definition: Let be an essential closed curve and denote its length.

Natural map:

Theorem The shortest representative for a non trivial homology class is always a multiple of a closed simple geodesic.

• important monotone increasing on

Aigner's conjectures proof

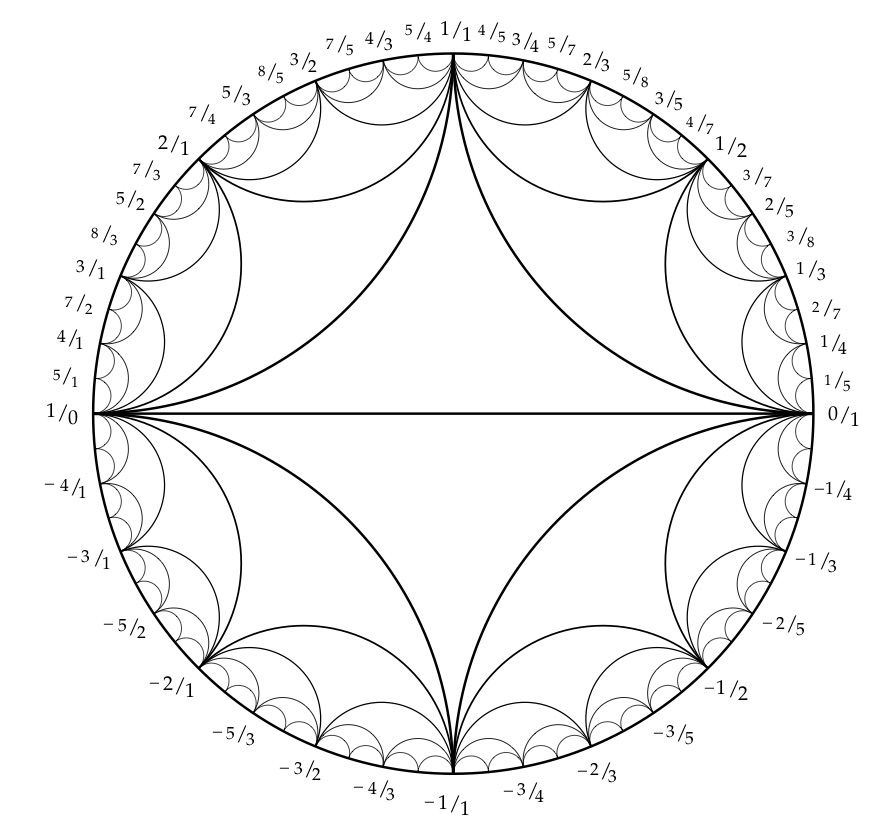
Labeling Markoff numbers

• Markoff number =
• Farey "tree" of coprime integers
• Markoff tree of solutions to the cubic
• Bass-Serre tree of a free product
• Mapping class group of the torus

Tree structure for triples

comes from Bass-Serre tree of

arcs

• simple closed geodesic
• arc on a punctured torus(disjoint from the closed geodesic)
• -lengths of arc

Farey diagram

• arc
• Farey neighbors iff
• obvious transitive action on Farey neighbors

-lengths

Definition

arc = Poincaré geodesic joining

• -length of arc
• -length of arc on
  or is the length of a lift to

Ptolemy identity

Ptolemy identity is homogeneous

• (Ptolemy)
• -lengths only defined up to a multiplicative constant

• ie a choice of horoballs based at the parabolic points

source

source

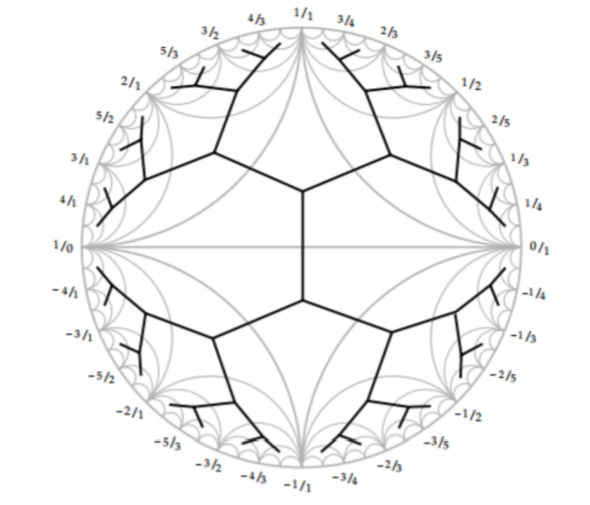
Tree structure

comes from Bass-Serre tree of

Role of the character variety

H. Cohn Approach to Markoff’s Minimal Forms Through Modular Functions (1955)

• modular torus = quotient of upper half plane by commutator subgroup of , acting by Mobius transformations
• relates Markoff numbers to lengths of simple closed geodesics

• modular torus = quotient of upper half plane by commutator subgroup of

• length geodesic
• -length arc
• after normalising

Character variety

modular torus =

• fundamental group of the torus

• representation

• Definition character map

• loop round puncture

Theorem: (Cohn and many others) The semi-algebraic set:

• identified with the Teichmueller space of the punctured torus.

• group of the automorphisms is induced by the action of the mapping class group

• the permutation

• the (Vieta) involution

• recursively enumerate lengths all simple closed curves

• roots satisfy both Vieta relations
• (trace)
• (Ptolemy)

Lemma A:

• Proof:

• (trace)

• (Ptolemy)

• normalise so that -lengths are then do an induction

(Geometric) uniqueness conjecture

The multiplicity of any number in the complementary regions to the tree is at most 6.

Button's Theorem and -lengths

Button's Theorem

If is a Markoff number which is prime
then there is a unique triple

Theorem (Fermat)

Let be a prime then has a solution over iff

2. is a multiple of 4.

• Button's theorem follows from "unicity" of
• unique factorisation
• The multiplicity of any number in the complementary regions to the tree is at most 6

Why 6?

and

• modular torus
• loop around the cusp
• automorphism group
• "generator" of the automorphism group is
• normalises so induces an involution of
• := elliptic involution has 3 fixed points which lift to the orbit of i.

• elliptic involution swaps triangles fixes midpoint of diagonal
• normalises induces an involution of
• the fixed points lift to the

Ford circles

orbit of are the Ford circles

• orbit of are the Ford circles

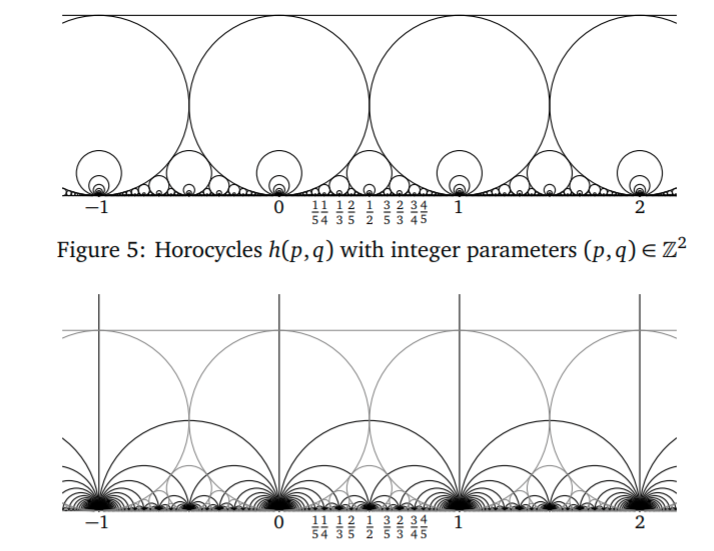
Proposition (Penner)

• arc joining has -length
• -length = length of the portion outside Ford circles tangent to the real line at its endpoints

Corollary

If one of the Ford circles is then
the midpoint of the arc is at Euclidean height

Corollary

One of the Ford circles is then
the midpoint of the arc is at Euclidean height

blue arc unique arc disjoint from blue curve

Lemma A'

Normalisation, fundamental triple
.

Corollary B

Every Markoff number is a sum of squares ie

Geometric proof of Corollary B

• simple close geodesic is invariant under the elliptic involution
• the unique arc disjoint from is invariant
• a fixed point of the elliptic involution on
• a lift of which is a vertical line and which meets
• since -length of = m this point is at euclidean height

and so we have the equation

by the same argument....

Lemma C Let be a positive integer.
The "number of ways" of writing as
with coprime,
is equal to the number of arcs satisfying:

joins to
integers and coprime
arc meets the orbit

Counting solutions

The "number of ways" of writing as .

• four choices for the signs
• swap and , only swapping "counts"

• Example:

Lemma C' Let be a positive integer.
The "number of ways" of writing as
with coprime,
is equal to the number of arcs

1. on the modular surface
2. of -length
3. which pass through the cone point of of order 2.

Corollary B

Every Markoff number is a sum of squares ie

Recursion for (complex) Markoff numbers

(Ptolemy)

In fact the Ptolemy relation factorises over

yields a recursion for a set of Gaussian integers
such that each Markoff number is the norm of

• Example: Fibonacci numbers

Fibonacci numbers

x, y = 1 + 0J, 1 + 1J

fib = []
for k in range(10):
    z = y*y.conjugate() + 1J
    u = x*z/ (x*x.conjugate())
    fib.append(f'{u}')
    x, y = y, u
    
' '.join(fib)

• Just showing that .

Back to Button exactly 6 simple arcs of -length on

Proof of Button

every Markoff number is the sum of two squares

• if is prime then there are two ways of doing this
• there are oriented simple arcs of length on
• multiplicity of in the Markoff tree

Sums of squares

Button's Theorem

If is a Markoff number which is prime

then there is a unique triple

• in
• in
• or is a multiple of 4.

Theorem F1: Let be a prime then

has a solution over
if or is a multiple of 4.

Theorem F2: Let be a prime then

has a solution over
iff or is a multiple of 6.

Theorem F3: Let be a prime then

has a solution over
if .

• arcs of -length on
• immersed ideal triangles of -length on
• arcs of -length on

An immersed ideal triangles with sides of -length on

two groups of order 4

Acting on

Acting on

Zagier

Burnside Lemma

• acting on then

• := fixed points of the element

• := the orbit space.

• proposition
  If is a prime of the form
  then has a solution over
• Follows from Wilson's Theorem

"Geometric" proof: Group acting on :

• Count fixed points

• identity

• ?

Apply Burnside

• if p=1 mod 4, then

Theorem F2: sum of 2 squares

Acting on or the Farey diagram
or on the arcs of

• three punctured sphere
• standard fundamental domain

• = pair of ideal triangles
• all edges -length 1

are midpoints of 3 arcs
of -length 1

• fixed point of 3 different involutions
• one dotted arc has -length
• other dotted arc has -length

Lemma C'

Let be a positive integer.
The "number of ways" of writing as a sum of squares

with coprime integers is equal to the number of arcs

coprime to which meet

subgroup of automorphisms
fixing the cusp labeled :

• a reflection that
  swaps
  fixes the arc of -length = 2
• another reflection that
  fixes
  fixes the arc of -length = 1
• both fix the midpoint

group lifts to

• fixes

The set

• arcs joining cusps with -length
• "lift to vertical lines" with endpoints
• as before

Fixed points I

First the automorphism

• fixes
• fixes the arc of -length = 1
• swaps the upper and lower ideal triangles
• has no fixed points in

The automorphism induced by
fixes two and exactly two arcs in .

Can then apply Burnside Lemma to prove Theorem F2

• Proof:
• suppose that there is an invariant arc that starts at
• then it must end at
• its - length is
• prime two solution
  

Questions/Remarks

Can other elementary results for quadratic forms?

• if is a multiple of 6.
  using immersed "equilateral" ideal triangles.

• (Elsholtz) if
  using arcs where

• Baragar ? m, 3m - 2, 3m + 2 prime

• More detailed analysis of the spectrum of -lengths?
  Orthotree, orthoshapes and ortho-integral surfaces
  Nhat Minh Doan