Surface automorphisms and elementary number theory

greg mc shane

• elementary number theory
• hyperbolic geometry
• try not to talk about continued fractions

• some is joint work with V. Sergiescu
• two index 6 subgroups
• three punctured sphere, automorphisms
• modular torus, automorphisms

Problem 0

Problem 1

Markoff numbers are integers that appear a Markoff triple

which are solutions of a Diophantine equation
the so-called Markoff cubic

Odd index Fibonacci numbers are Markoff numbers

Frobenius uniqueness conjecture

The largest integer in a triple determines the two other numbers.

• Only partial results
• m = Markoff number = z > y > x

• Jack Button for m prime
• Zhang An elementary proof...
• Lang, Tan A simple proof....
• Baragar m, 3m - 2, 3m + 2 prime

Problem 2:

Give a geometric proof of

If a prime and 4 divides then
for coprime integers .

References etc

• First proof Euler (reciprocity, descent)
• Heath-Brown, Fermat’s two squares theorem. Invariant (1984)
• Zagier, A one-sentence proof that every prime p = 1 (mod 4) is a sum of two squares, 1990
• Dolan, S., The Mathematical Gazette, 106(564). (2021)
• Elsholtz, Combinatorial Approach to Sums of Two Squares and Related Problems. (2010)

Zagier: one sentence

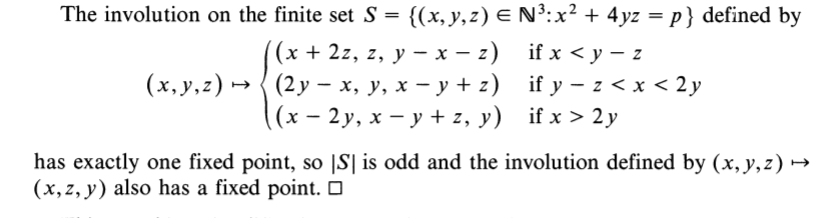
Problem 3:

Martin Aigner

• Proofs from THE BOOK
• 100 years of uniqueness
• Convexity and Aigner's Conjectures
• Prove his conjectures with one figure?

There is a natural map (we'll see why shortly)

Aigner's conjectures proof

Sketch of proof

Definition: Let be an essential closed curve and denote its length.

Natural map:

Theorem The shortest representative for a non trivial homology class is always a multiple of a closed simple geodesic.

• important monotone increasing on

Aigner's conjectures proof

Labeling Markoff numbers

A tale of trees

• Markoff number =
• Farey "tree" of coprime integers
• Markoff tree of solutions to the cubic
• Bass-Serre tree of a free product
• Mapping class group of the torus

coprime integers

• closed geodesic
• arc on a punctured torus(disjoint from the closed geodesic)
• -lengths of arcs

• arc
• Farey neighbors iff
• obvious transitive action on Farey neighbors

source

source

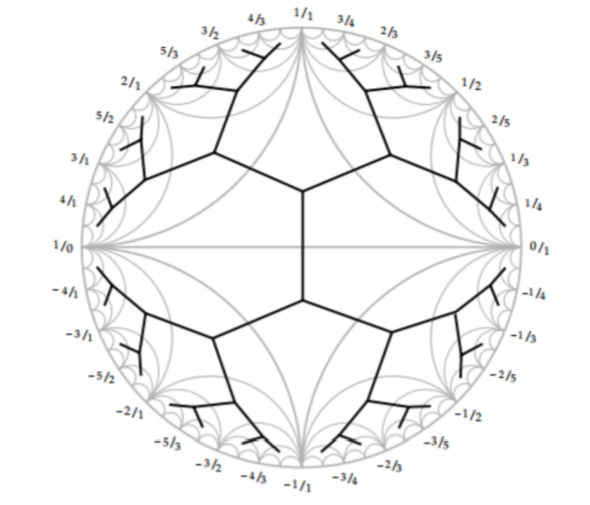
Tree structure

comes from Bass-Serre tree of

Role of the character variety

H. Cohn Approach to Markoff’s Minimal Forms Through Modular Functions (1955)

• modular torus = quotient of upper half plane by commutator subgroup of , acting by Mobius transformations
• relates Markoff numbers to lengths of simple closed geodesics

• modular torus = quotient of upper half plane by commutator subgroup of
• obtained from a pair of ideal triangles by identification
• elliptic involution swaps triangles fixes midpoint of diagonal

Character variety

modular torus =

• fundamental group of the torus.
• any hyperbolic torus = ,
• discrete faithful representation
• lifts to
• generators of
• Definition character map

Theorem: (Cohn and many others) The semi-algebraic set:

• identified with the Teichmueller space of the punctured torus.

• group of the automorphisms is induced by the action of the mapping class group

• the permutation

• the (Vieta) involution

Uniqueness conjecture

• The largest integer in a triple determines the two other numbers.
• The multiplicity of any number in the complementary regions to the tree is at most 6

Simple representatives

• blue curve is simple representative of its homotopy class
• not every homotopy class contains a simple curve
• every (non trivial) homology class has a representative that is a (multiple) of a simple curve

Button's Theorem and -lengths

Button's Theorem

If is a Markoff number which is prime
then there is a unique triple

Theorem (Fermat)

Let be a prime then has a solution over iff

2. is a multiple of 4.

• Button's theorem follows from "unicity" of
• unique factorisation

Frobenius uniqueness conjecture

• The multiplicity of any number in the complementary regions to the tree is at most 6

and

• modular torus
• loop around the cusp
• automorphism group
• "generator" of the automorphism group is
• normalises so induces an involution of
• := elliptic involution has 3 fixed points which lift to the orbit of i.

• elliptic involution swaps triangles fixes midpoint of diagonal
• normalises induces an involution of
• the fixed points lift to the

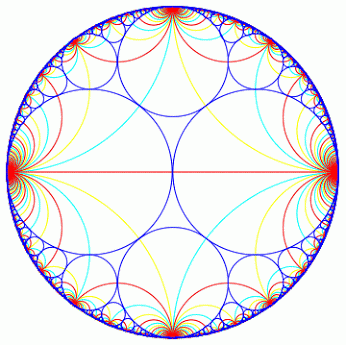
Ford circles

Ford circles

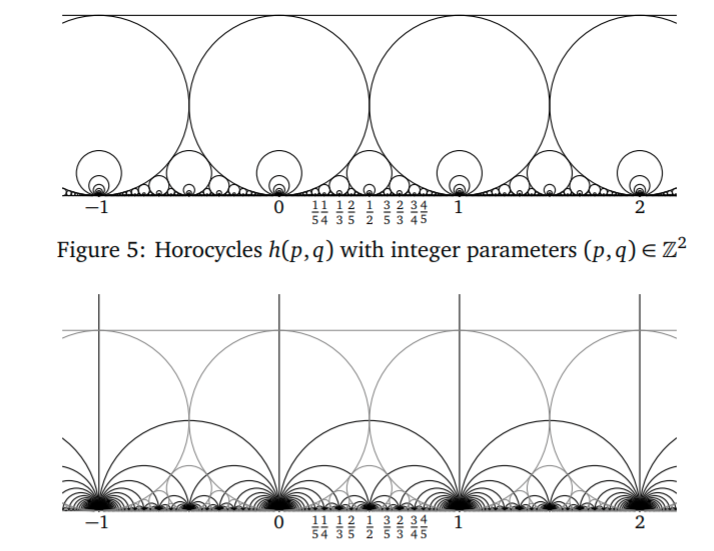
Definitions

arc = Poincaré geodesic joining

• -length of arc

• -length of arc on is the length of a lift to

• acts by Mobius transformations on

• orbit of are the Ford circles

• point of tangency with , diameter =
• hyperbolic midpoint of the arc joining to this Ford circle is at euclidean height

• point of tangency with , diameter =
• hyperbolic midpoint of the arc joining to this Ford circle is at euclidean height

Proposition (Penner)

• arc joining has -length
• -length = length of the portion outside Ford circles tangent to the real line at its endpoints

transitive on ,

• can suppose and
• joins Ford circle tangent at and another of diameter
• hyperbolic length of portion outside these is

pairing arcs and curves

• modular torus obtained from a pair of ideal triangles by identification
• blue arc is the unique arc disjoint from blue curve

Lemma A

The -length of the unique arc disjoint from the
simple closed geodesic such that is .

Proof: Easy calculation

Corollary B

Every Markoff number is a sum of squares ie

Geometric proof of corollary

• simple close geodesic is invariant under the elliptic involution
• the unique arc disjoint from is invariant
• a fixed point of the elliptic involution on
• a lift of which is a vertical line and which meets
• since -length of = m this point is at euclidean height

and so we have the equation

by the same argument....

Lemma C

Let be a positive integer.
The "number of ways" of writing as a sum of squares

with coprime integers is equal to the number of arcs

coprime to which meet

Counting solutions

The "number of ways" of writing as

• eight solutions
• four choices for the signs
• swap and
• only swapping "counts"

Example

Lemma C'

The number of ways of writing as a sum of squares

is equal to the number of arcs on the modular surface

1. of -length
2. which pass through the cone point of of order 2.

exactly 6 simple arcs of -length on

Proof of Button

every Markoff number is the sum of two squares

• if is prime then there are two ways of doing this
• there are oriented simple arcs of length on
• multiplicity of in the Markoff tree

Sums of squares

Button's Theorem

If is a Markoff number which is prime

then there is a unique triple

• in
• in
• or is a multiple of 4.

Theorem F1: Let be a prime then

has a solution over
iff or is a multiple of 4.

Theorem F2: Let be a prime then

has a solution over
iff or is a multiple of 6.

two groups of order 4

Acting on

Acting on

Zagier

Let's begin then...

Burnside Lemma

• acting on then

• := fixed points of the element

• := the orbit space.

• proposition
  If is a prime of the form
  then has a solution over
• Follows from Wilson's Theorem

"Geometric" proof: Group acting on :

• Count fixed points

• identity

• ?

Apply Burnside

QED

Theorem F2: sum of 2 squares

Acting on or the Farey diagram
or on the arcs of

• three punctured sphere

• standard fundamental domain
• = pair of ideal triangles
• all edges -length 1

are midpoints of 3 arcs
of -length 1

• fixed point of 3 different involutions
• one dotted arc has -length
• other dotted arc has -length

Lemma C'

Let be a positive integer.
The "number of ways" of writing as a sum of squares

with coprime integers is equal to the number of arcs

coprime to which meet

subgroup of automorphisms
fixing the cusp labeled :

• a reflection that
  swaps
  fixes the arc of -length = 2
• another reflection that
  fixes
  fixes the arc of -length = 1
• both fix the midpoint

group lifts to

• fixes

The set

• arcs joining cusps with -length
• "lift to vertical lines" with endpoints with odd
• as before

Fixed points I

First the automorphism

• fixes
• fixes the arc of -length = 1
• swaps the upper and lower ideal triangles
• has no fixed points in

The automorphism induced by
fixes two and exactly two arcs in .

• can thencan then apply Burnside Lemma to prove Theorem F2

• Proof:
• suppose that there is an invariant arc that starts at
• then it must end at
• its - length is
• prime two solution

Questions/Remarks

Can other elementary results for quadratic forms?

• if is a multiple of 6.
  using immersed "equilateral" ideal triangles.

• (Elsholtz) if
  using arcs where

• Baragar ? m, 3m - 2, 3m + 2 prime

• More detailed analysis of the spectrum of -lengths?
  Orthotree, orthoshapes and ortho-integral surfaces
  Nhat Minh Doan