\(\sum\frac{1}{1 + e^{\ell_\gamma}}=\frac{1}{2}\)

Is a formula but it is describing a geometric truth

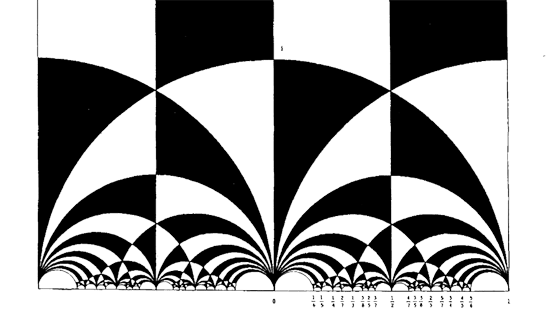
Illustrator 88 circa 1990

Apologies

This was hacked together

• in nvim
• using Markdown
• and revealjs

and my first time on Zoom :(

Undergrad Surfaces

2 dimensional space (manifold)

• disc (is a subset of)
• plane (is the image under the stereographic projection of)
• sphere
• torus (which is a branched cover of the sphere)

Study them by embedding
them in \(\mathbb{R}^3\).

Coordinates

• disc (polar)
• plane (cartesian or polar)
• sphere (spherical polar \(0 \leq \theta \leq \pi, 0\leq \phi\leq 2\pi\))
• torus (spherical polar \(0 \leq \theta \leq 2\pi, 0\leq \phi\leq 2\pi\))

Grew out of this..

Geometry

Three questions

• what are the isometries?
• what are the geodesics?
• what are the optimal maps to other spaces?

Torus

The disc, plane and sphere are simply connected.
Torus is not simply connected.

• Fundamental group is isomorphic to \(\mathbb{Z}^2\)
• Is a quotient of the plane by a group of translations \(\Gamma\) generated by...
• \(z \mapsto z + 1\) and \(z \mapsto z + \tau\) where \(\tau \in \mathbb{H} \subset \mathbb{C}\)

making a torus

from a parallelogram with corners \(0, 1, 1 + \tau, \tau\)
by glueing opposite edges

Tilings/tessalations

source

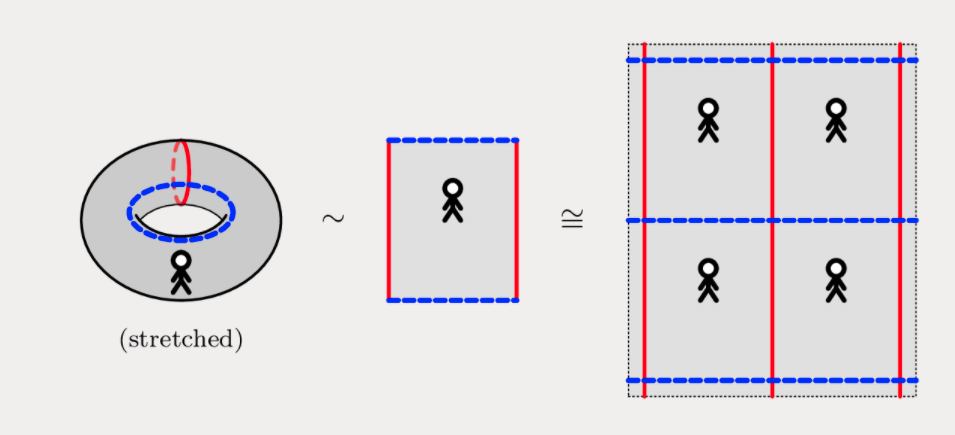
Tilings/tessalations

Geodesics

Geodesic = length minimising curve

• straight line in the (euclidean) plane
• great circle on the sphere

Geodesic foliation: \(\mathbb{R}^2\) is partitioned by parallel families of geodesics.

Geodesics on the flat torus

Being geodesic is a local property so under the projection map straight lines map to geodesics
\((\theta, \phi) \mapsto (e^{i\theta},e^{i\phi})\), \(\mathbb{R}^2 \rightarrow \mathbb{R}^2 / \Gamma\) = torus

Long term behavior

• rational slope => closed
• irrational slope => dense

Geodesics on the flat torus

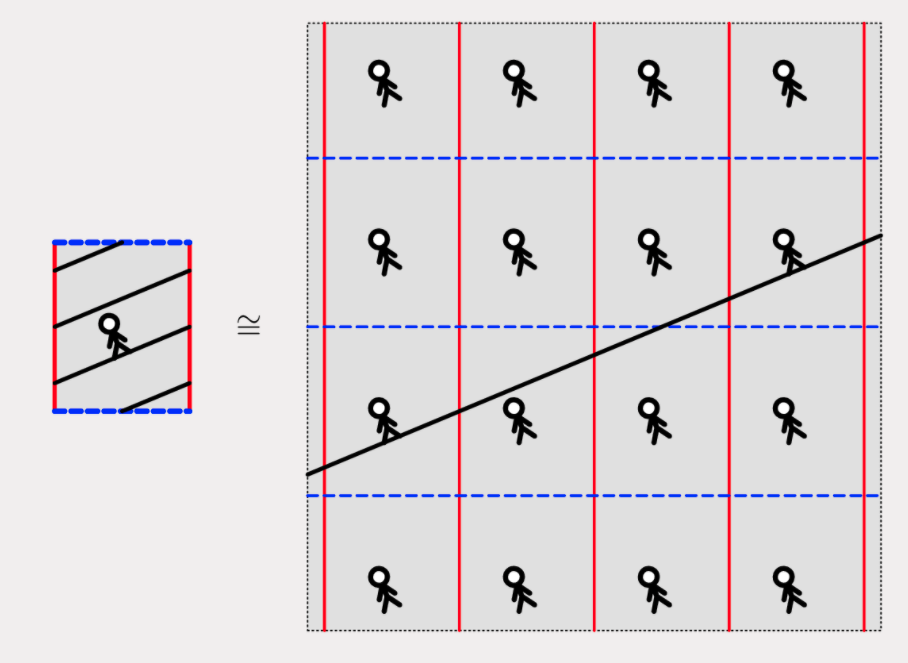
Geodesics on the flat torus

• closed geodesic \(\gamma\), rational slope = p/q,
• where \(p,q\) are coprime integers
• length of the geodesic is \(\ell_\gamma = | p \tau + q |\)
• this is a closed formula for the length of a closed geodesic

Let's draw some

to see how they fill outspace

Farey enumeration

Recursive enumeration coprime pairs \(p,q\)

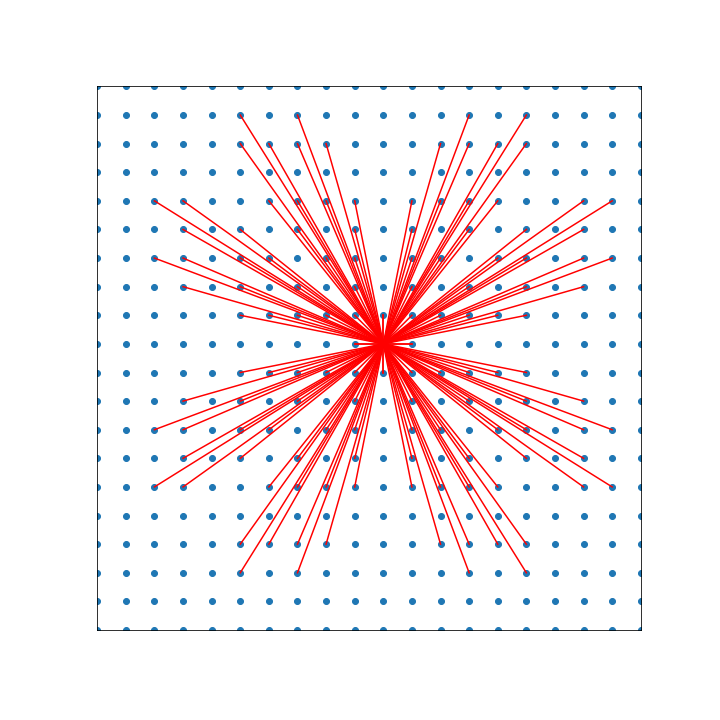
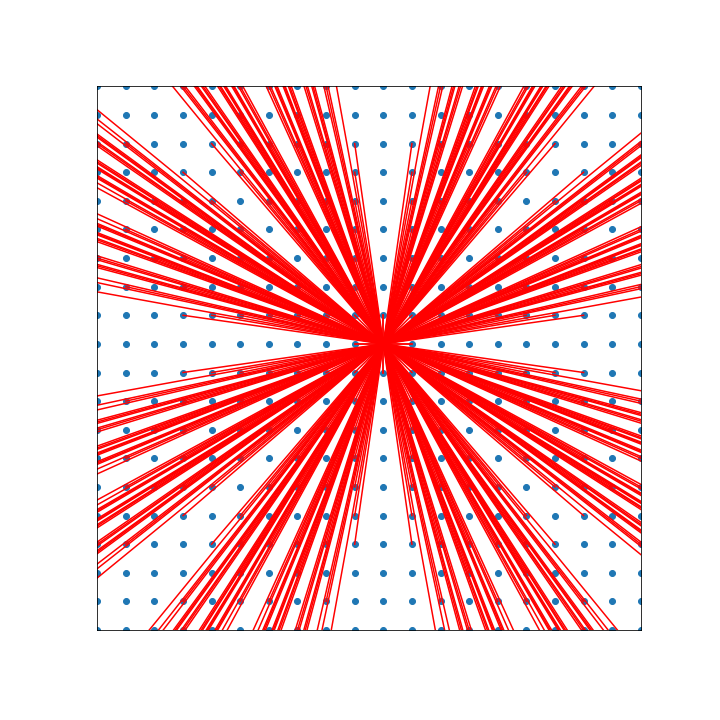
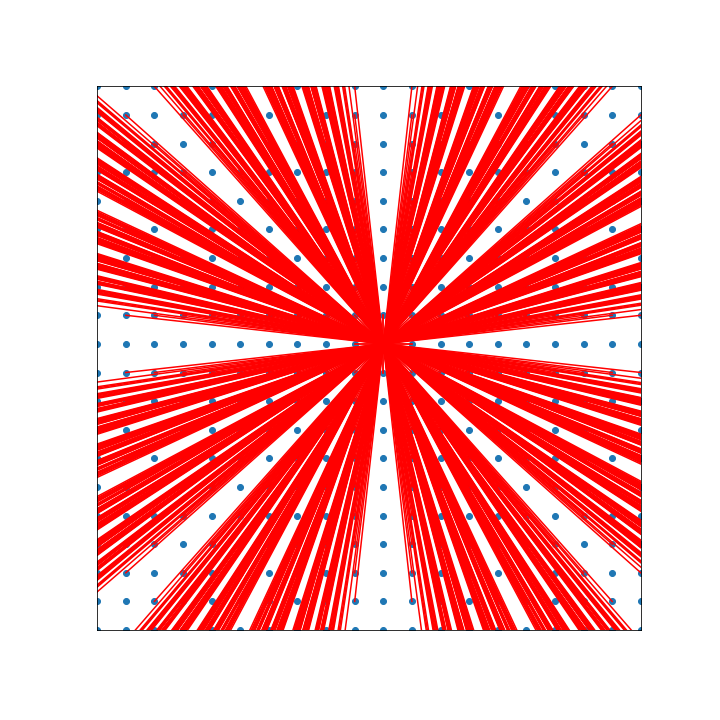
There are holes but they will get filled in

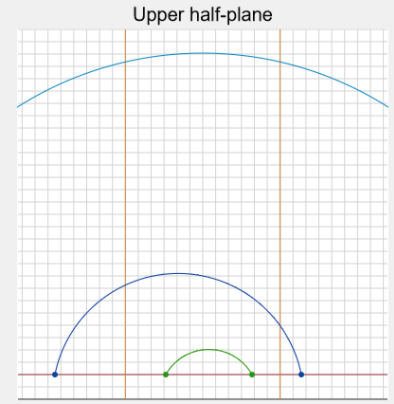
Poincare disc/upper half plane

metric for which the orientation preserving isometries are Moebius transformations : \(z \mapsto \frac{a z + b }{cz + d}\)

Call of Cthulhu

the geometry of the dream-place he saw was abnormal, non-Euclidean, and loathsomely redolent of spheres and dimensions apart from ours.

Ideal triangles

area = \(\pi\), all angles = 0

Types of isometry

\(z \mapsto \frac{a z + b }{cz + d}\)

• rotations : single fixed point in \(\mathbb{H}\)
• parabolic : single fixed point on \(\mathbb{R}\)
• loxodromic : pair of fixed points on \(\mathbb{R}\)

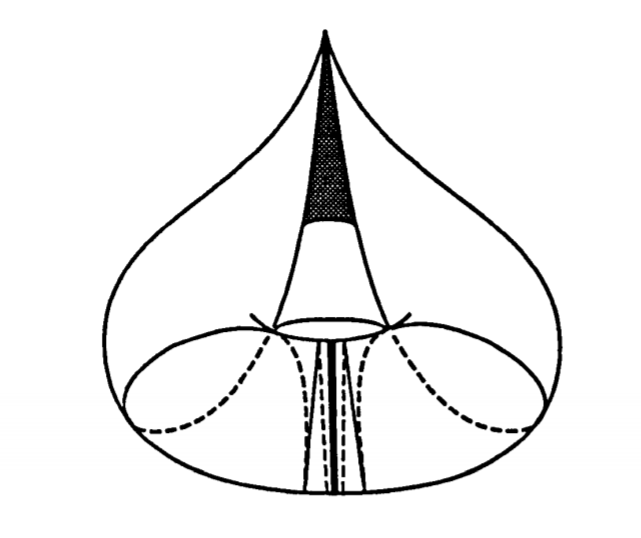
Punctured torus

Glue opposite sides ideal quadrilateral.

Punctured torus

• closed geodesics
• dense geodesics
• all sorts of other geodesics

on the left simple, on the right non simple

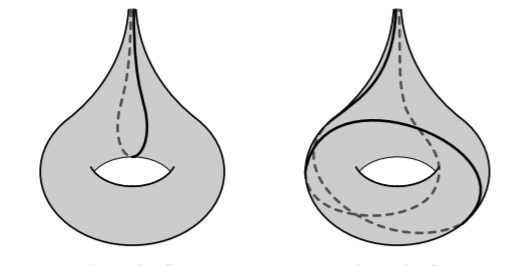
most geodesics aren't simple they have self intersections.

81 shortest geodesics on torus

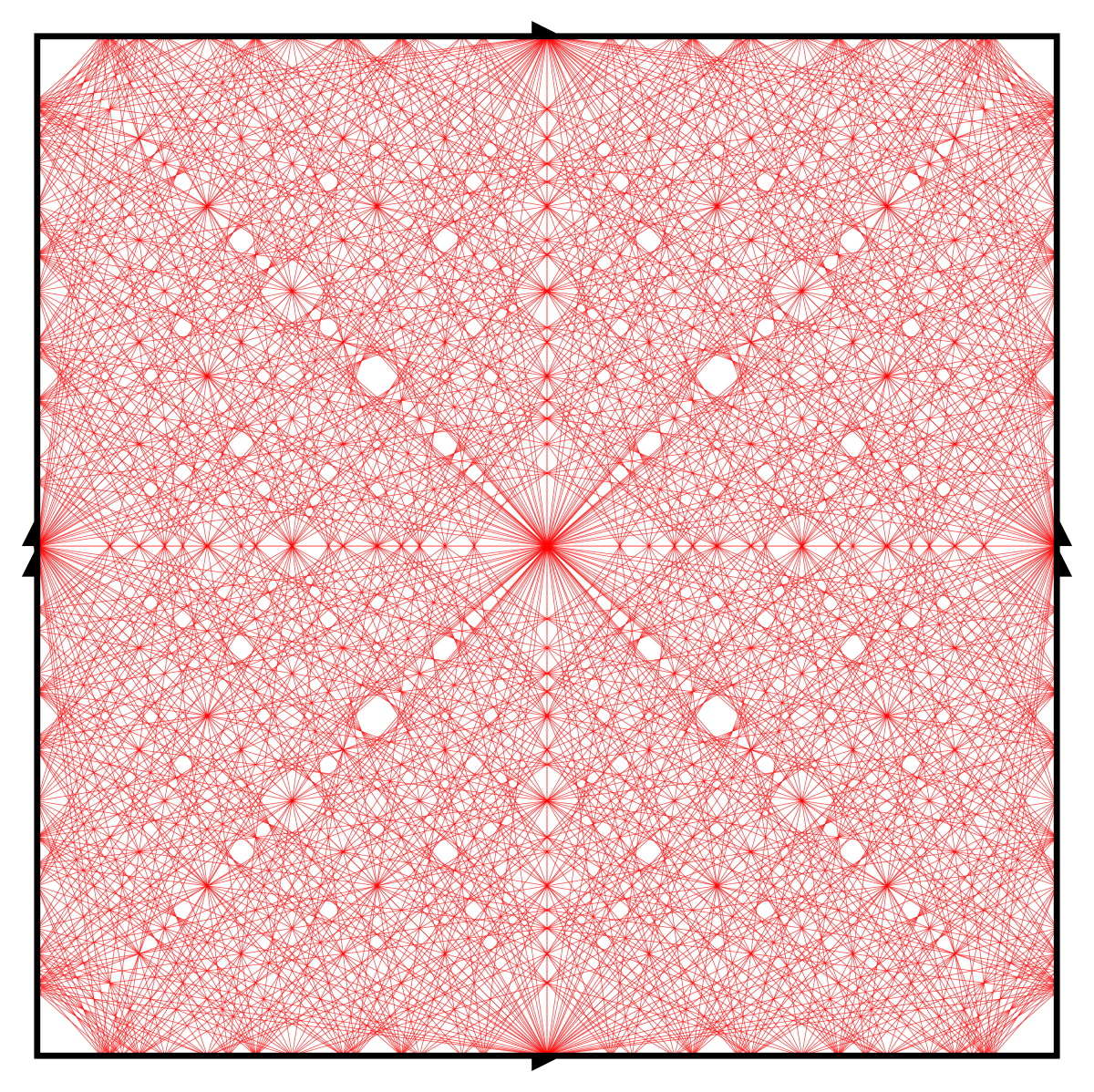
on punctured torus

Birman-Series Theorem

The union of all complete simple geodesics is

• closed
• nowhere dense i.e. there are holes
• Hausdorff dimension 1, so measure zero

Big question: where are the holes?

Pseudo sphere embedded in \(\mathbb{R}^3\). \((\mathrm{sech}(u)\cos(v),\mathrm{sech}(u)\sin(v),u-\tanh(u) )\)

Pseudo sphere as a quotient

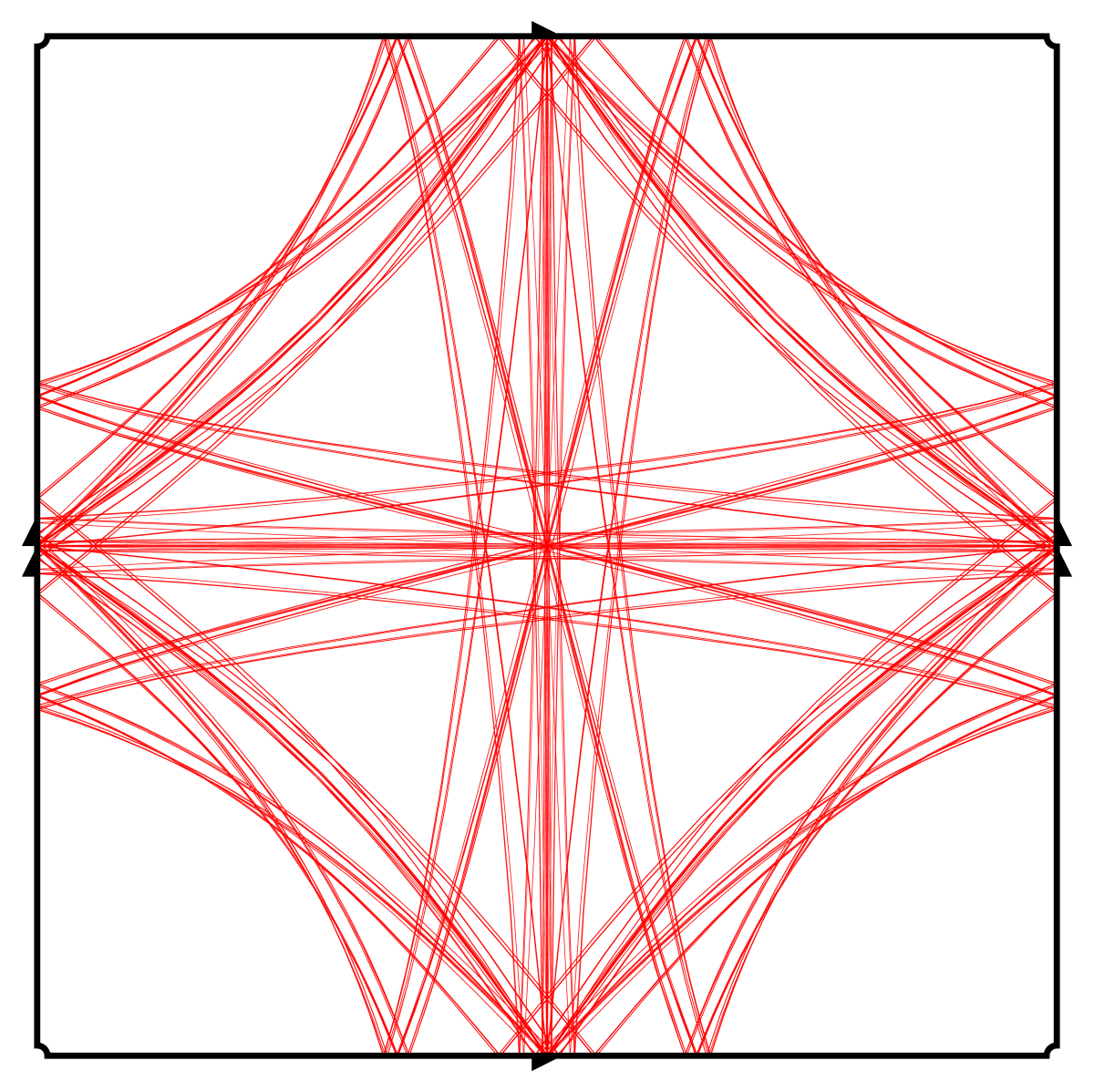
Observation

The pseudo sphere is foliated by vertical geodesics

Fundamental lemma

• every punctured torus contains a pseudo sphere of area 1
• no simple closed geodesic enters this pseudo sphere
• any simple geodesic that enters the pseudo sphere is vertical

The pseudo sphere is a bit like a black hole once past it's horizon there is no escape for the geodesic.

Historical background

• Approach to Markoff's Minimal Forms Through Modular Functions Harvey Cohn dowload
• Geometry of the Markoff numbers dowload
• Markov numbers wiki

Intersection of Birman Series set with pseudo sphere.

\(K \times \mathbb{R}^+ = K_{ess} \sqcup K_{iso}\)

• \(K\) = closed nowhere dense subset of circle
  
• \(K_{iso}\) = isolated points
• "shallow" points in closure of interval \(\subset K_{ess}^c\)
• also "deep" points in \(K_{ess}\)

\(\frac{2}{1 + e^{\ell_\gamma}}\)

is the length of an interval in \(K_{ess}\)

geometrically

what are the geodesics like that come from

• isolated points
• "shallow" points?
• "deep" points?

My thesis

\(x \in K \rightarrow \gamma_x\) the geodesic "accumulates" somewhere.

Surface cut along accumulation set

Classification Theorem

• \(\gamma_x\) returns to pseudo sphere <=> x isolated
• \(\gamma_x\) spirals to a closed geodesic <=> x "shallow"
• otherwise x "deep"

Corollary

The gaps in \(K_{ess}\) are 1-1 with closed geodesics

Short story

• Look what I proved I think you're going to like it.
• Either false or Bob Penner has done it already

Short story

Markoff numbers

(Cohn) the Markoff numbers are \(2/3 \cosh(\ell_\gamma/2)\) for \(\gamma\) a closed simple geodesic on the punctured torus.

• recursive enumeration, no closed formula

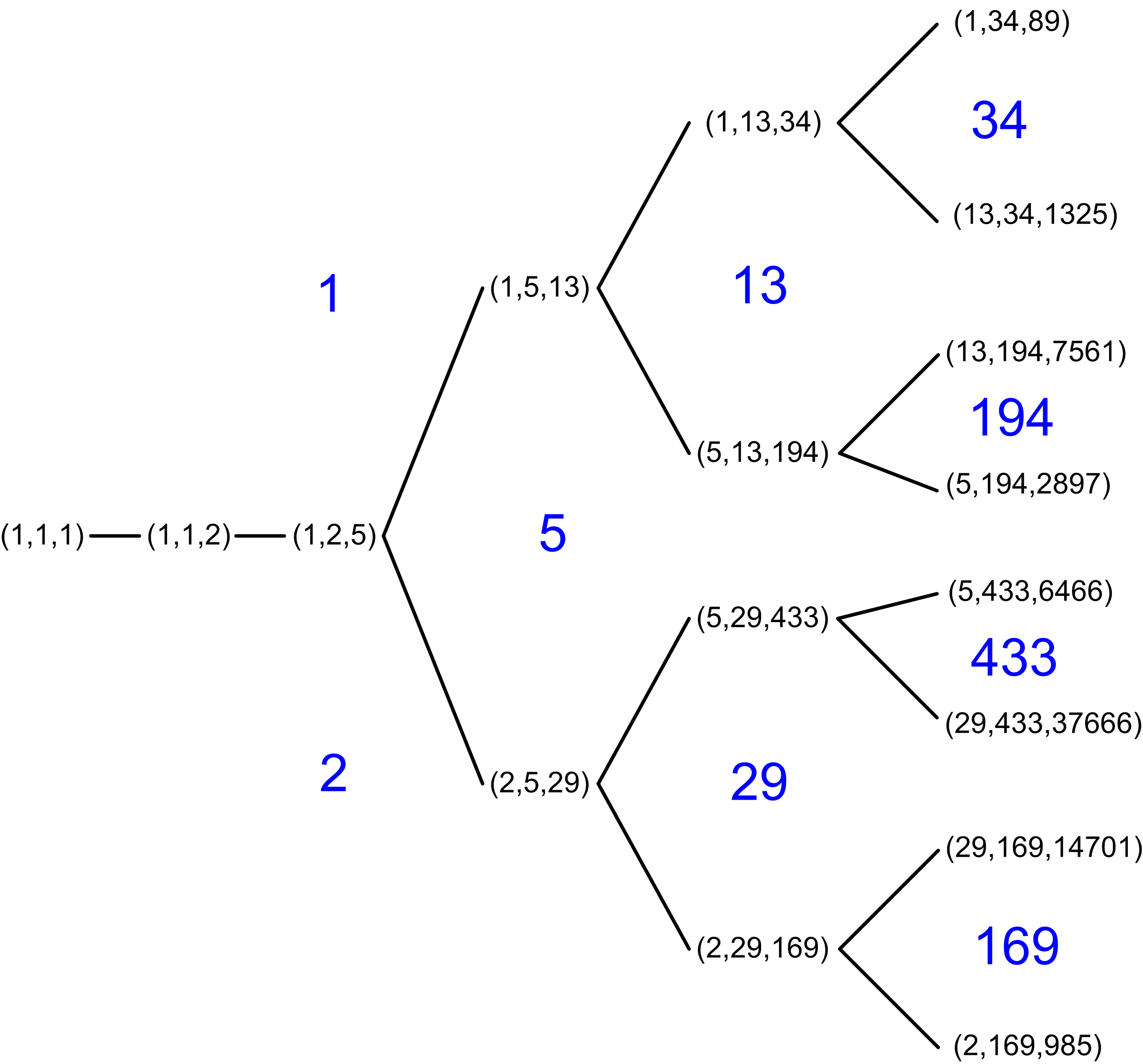
I wrote a program

Diophantine approximation

• x "deep" point not isolated or shallow
• Even-numbered convergents are smaller than the original number,
• while odd-numbered ones are larger.

Applications :

partition of unity for integration

Teichmueller space

3 glueing parameters + 1 relation Shear coords

Teichmueller space

2 parameters - length and twist

Fenchel Nielsen coords

References

Mirzakhani
Wright