%Geometry of sums of squares
%JSTeichR
%November 2022

• Geometry of Fermat’s sum of squares
• Convexity and Aigner's Conjectures
• Eisenstein integers and equilateral ideal triangles

• Proofs from THE BOOK{target="_blank"}
• Convexity and Aigner's Conjectures{target="_blank"}
• Can I prove these with one figure ?

• Geometry of Fermat’s sum of squares

Markov numbers are integers that appear in triples which are solutions of
a Diophantine equation the so-called Markov cubic

150

Theorem

can be identified with the Teichmueller space of the punctured torus
using Penner's -lengths.

Odd index Fibonacci numbers are Markoff numbers

Markoff numbers

Frobenius uniqueness conjecture

• The largest integer in a triple determines the two other numbers.
• For every Markoff number there are exactly 3 simple closed geodesics of length on the modular torus

Partial results

m = Markoff number

• Jack Button for m prime{target="_blank"}
• Zhang An elementary proof...{target="_blank}
• Baragar m, 3m - 2, 3m + 2 prime{target="_blank}
• Bugeaud, Reutenauer, Siksek{target="_blank}
• Conclusion too hard!!!

Button's Theorem

If is a Markoff number which is prime

then there is a unique triple

• in
• in
• or is a multiple of 4.

Theorem 1.2

Let be a prime then

has a solution over

• iff or is a multiple of 4.
• Button's theorem follows from unicity of

Theorem 1.3

Let be a prime then

has a solution over

• iff or is a multiple of 6.

• Eisenstein integers and equilateral ideal triangles

two groups of order 4

Acting on

Acting on

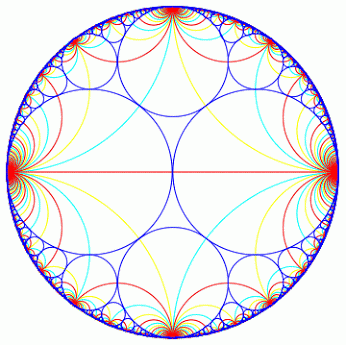
Farey tessalation

Ford circles

References etc

• Heath-Brown, Fermat’s two squares theorem. Invariant (1984)
• Zagier, A one-sentence proof that every prime p = 1 (mod 4) is a sum of two squares, 1990
• Elsholtz, Combinatorial Approach to Sums of Two Squares and Related Problems. (2010)
• Penner, The decorated Teichmueller space of punctured surfaces, Comm Math Phys (1987)
• Zagier text{target="_blank"}

Zagier

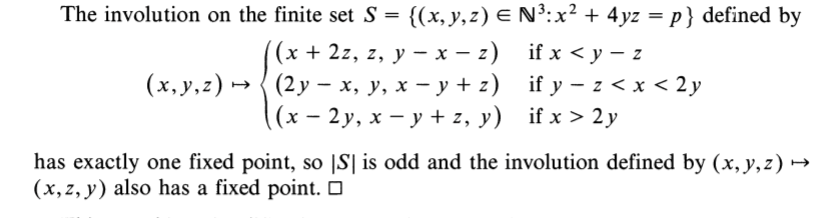
Let's begin then...

Burnside Lemma

• acting on then

• = fixed points of the element

• the orbit space.

Theorem 1.1

Let be a prime then

has a solution over

• iff or is a multiple of 4.

Proof

Group acting on :

Counting fixed points

• identity
• ?

Apply Burnside

QED

Theorem 1.2: sum of 2 squares

Acting on

Primitives

• infinitely many primitive elements
• primitive iff coprime
• transitive on primitives

Important

\begin{eqnarray*}
{ \textit{primitives} } &=& \mathbb{Q}\cup \infty\
&\subset& \text{circle/projective line } \
&=& \partial_\infty \mathbb{H}
\end{eqnarray*}

Farey tessalation

circle/projective line

• arc joining
• are Farey neighbors

source

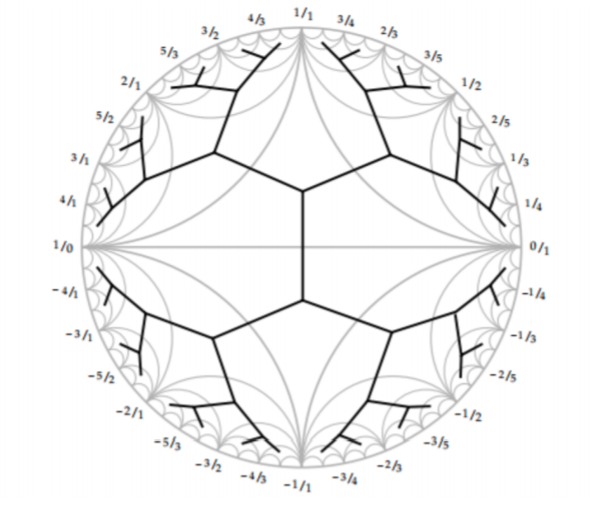
source

Definitions

• arc = Poincaré geodesic joining
• - length of arc

Lemma

-length = length of the portion outside Ford circles tangent to the real line at its endpoints

Ford circles

acts by Mobius transformations on

• preserves the Poincaré (hyperbolic) metric
• the orbit of are the Ford circles

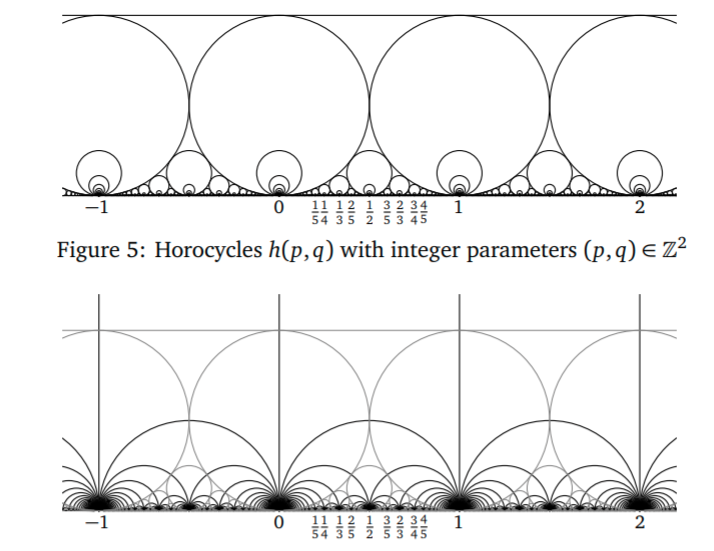
• point of tangency with , diameter =
• ie the diameter is the square of the inverse of the denominator of

Proof of lemma

• arc joining has -length
• -length = length of the portion outside Ford circles tangent to the real line at its endpoints

Proof of lemma

• transitive,
• can suppose and
• Ford circles tangent at
• and another of diameter

Groups and quotients

• has torsion so orbifold
• three punctured sphere
• once punctured torus

• For Aigner's conjectures the geometry of the
  simple geodesics on
  once punctured torus was important.
• For Fermat's theorem it's the automorphisms of
  = three punctured sphere

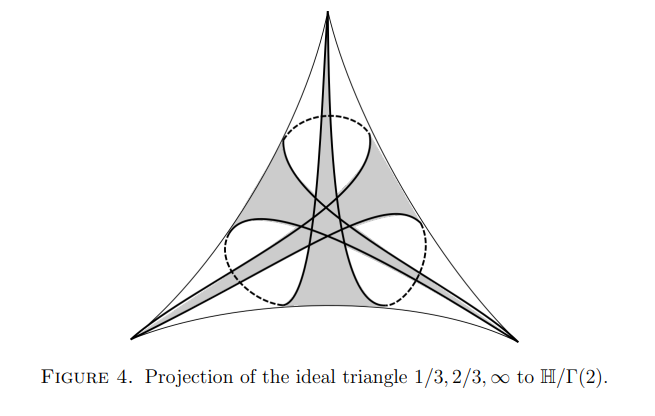
A three punctured sphere

can be cut up into 2 ideal triangles.

• Fundamental domain for

• are midpoints

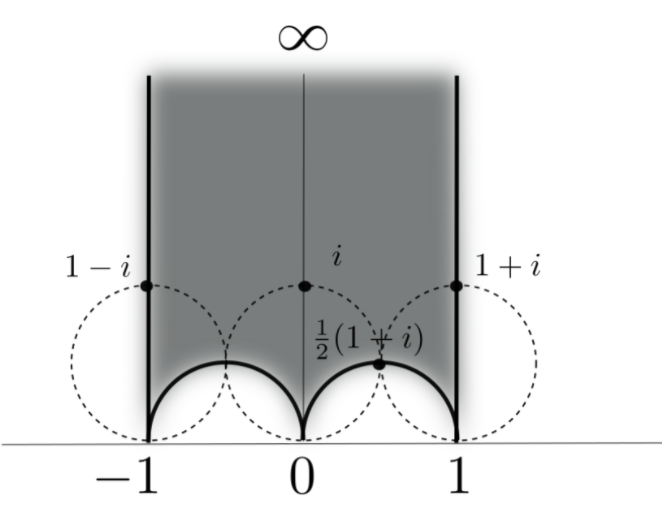
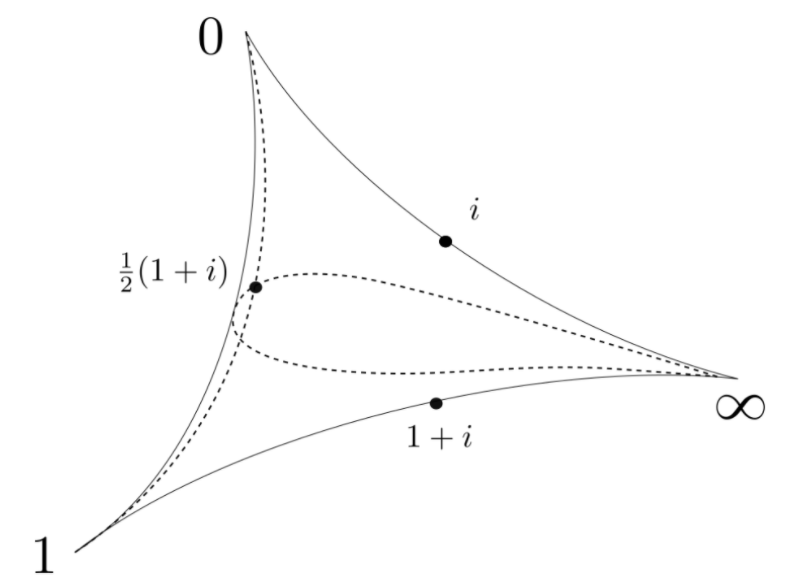
reciprocals of sums of squares

• are midpoints of arcs
• the lifts to of the midpoints

Lemma A

• Let be a positive integer.
• The number of ways of writing as a sum of squares with coprime integers
• is equal to the number of integers coprime to such that the line contains a point in the orbit of .

What is the group of automorphisms?

What is the subgroup of automorphisms

fixing the cusp labeled ?

• fixes the cusp and midpoint
  
• dashed arca are invariant under the group
  
• one arc has -length 1, the other 2.

the set

• arcs joining cusps with -length
• lift to vertical lines with endpoints with odd
• as before

Lemma A

Let be a positive integer.
The number of ways of writing as a sum of squares

with coprime integers is equal to the number of integers
coprime to
such that the line

contains a point in the orbit of .

subgroup lifts to

• fixes

automorphisms

• induces an automorphism no fixed points in
• is an inversion in a half circle with endpoints -1 and 1
• this arc's projection to surface is simple arc of -length

Lemma B

The automorphism induced by

fixes two and exactly two arcs in .

• apply Burnside Lemma to prove Theorem 1.2

Proof

• If and are exchanged by an inversion swapping Ford circles
• Then the endpoints of the fixed circle are and
• if the arc joining these points has -length =

Button's Theorem

If is a Markoff number which is prime

then there is a unique triple

• Button's theorem follows from unicity in
• unique vertical geodesic in Lemma A.
• let's look at that again

• Number of ways of writing as a sum of squares with coprime integers
• = number of integers coprime to such that the line contains a point in the orbit of .
• For every Markoff number there are exactly 6 simple closed geodesics of length on the modular torus
• exactly 6 simple arcs of -length on

.svg)

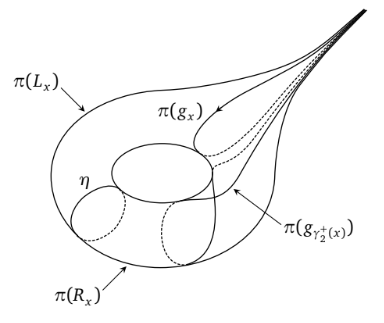
pair of disjoint simple closed and arc geodesics

Theorem

can be identified with the Teichmueller space of the punctured torus.

!
exactly 6 simple arcs of -length on

The End