Geometry of sums of squares

greg mc

Tokyo December 2021

proof with one figure ?

proof with one figure ?

hyperbolic geometry proof of

Proofs from the Book chapter

Some of this is joint work with
Vlad Sergesciu

motivation from Markoff

Markoff numbers are integers that appear in triples which are solutions of a Diophantine equation the so-called Markoff cubic

\(x^2 + y^2 + z^2 - 3x y z = 0.\)

\((1,1,1),(1,1,2),(1,2,5),(1,5,13)\)

Odd index Fibonacci numbers are Markoff numbers

\(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...\)

\((1,1,1),(1,1,2),(1,2,5),(1,5,13)\)

Markoff numbers

observation

  • Every integer appears to appear at most 6 times

Multiplicity \(\leq 6\)

Notation

  • \(\Gamma = \mathrm{SL}(2,\mathbb{Z})\) has torsion so \(\mathbb{H}/\Gamma\) orbifold
  • \(\Gamma(2) = \ker (\mathrm{SL}(2,\mathbb{Z})\rightarrow \mathrm{SL}(2,\mathbb{F}_2))\)
  • \(\Gamma' = [\Gamma,\Gamma]\)
  • \(\mathbb{H}/\Gamma(2)\) three punctured sphere
  • \(\mathbb{H}/\Gamma'\) once punctured torus

Frobenius uniqueness conjecture

Partial results

\(m\) = Markoff number

Button’s Theorem

If \(z\) is a Markoff number which is prime
then there is a unique triple \(z > y > x\)

\(x^2 + y^2 + z^2 - 3x y z = 0.\)

  • so when we take congruences in \(\mathbb{F}_z\)
    • \(\bar{x}^2 + \bar{y}^2 = 0\)
    • \((\bar{x}/\bar{y})^2 = -1\)

  • Button’s theorem follows from unicity of
    the sum of squares decomposition

two groups of order 4

Acting on \(\mathbb{F}_p^*\)

\(\begin{array}{lll} x &\mapsto& -x \\ x &\mapsto& 1/x \end{array}\)

Acting on \(\mathbb{H}\)

\(\begin{array}{lll} z &\mapsto& -\bar{z} \\ z &\mapsto& 1/\bar{z} \end{array}\)

arcs on a puntured sphere \(\mathbb{H}/\Gamma\)

Farey tessalation

arcs on the 3 punctured sphere

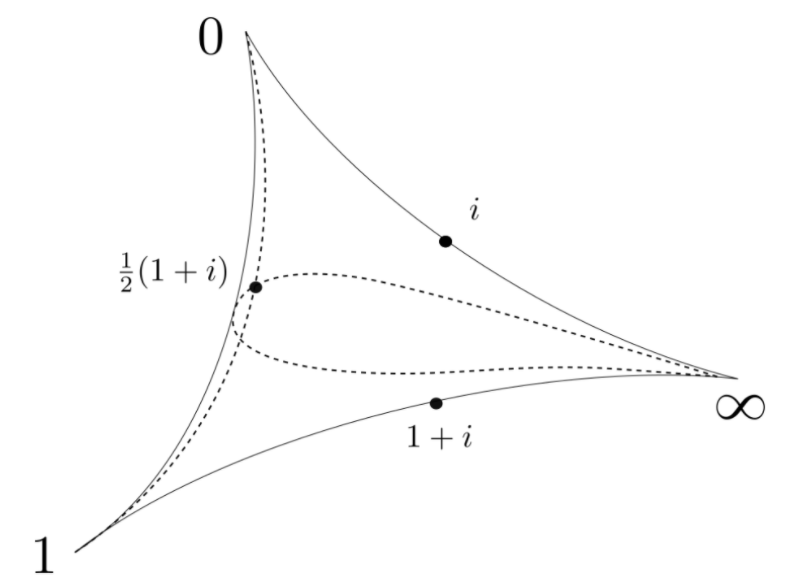
  • \(i, 1+i, \frac12 ( 1 + i)\) are midpoints

Ford circles

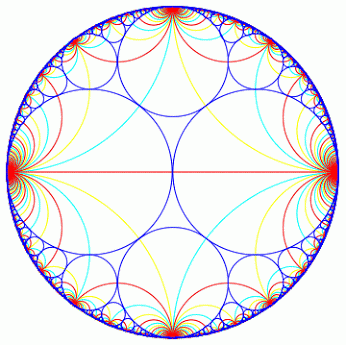
Ford circles

Bonahon’s video

References etc

Zagier

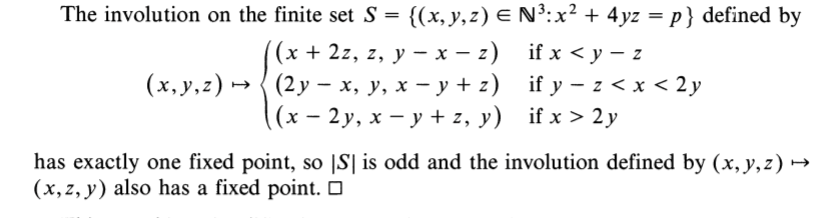
Let’s get started

Burnside Lemma

  • \(G\) acting on \(X\) then

    \(|G| |X/G| = \sum_{g} |X^g|\)

    • \(X^g\) = fixed points of the element \(g\)
    • \(X/G\) the orbit space.

Theorem 1.1

Acting on \(X = \mathbb{F}_p^*\)

  • identity \(|X^g| = p-1\)
  • \(x \mapsto -x, |X^g| = 0\)
  • \(x \mapsto 1/x, |X^g| = 2\)
  • \(x \mapsto -1/x, |X^g| = \ldots\)

…calculation

  • \(|G| |X/G| = \sum_{g} |X^g|\)
  • \(4 |X/G| = (p-1) + 2 + |X^{(x\mapsto -1/x)}|\)
    • so \(4\) doesn’t divide \((p+1)\)
    • \(\Rightarrow |X^{(x\mapsto -1/x)}|= 2\)
    • \(\Rightarrow \exists x,\, x^2 = -1\)

adapting for Fermat

Theorem 1.2: sum of 2 squares

Acting on \(\mathbb{H}\)

\(\begin{array}{lll} z &\mapsto& -\bar{z} \\ z &\mapsto& 1/\bar{z} \end{array}\)

Primitives

  • infinitely many primitive elements in \(\mathbb{Z}^2\)
  • \((a,b)\) primitive iff \(a,b \in \mathbb{Z}\) coprime
  • \(SL(2,\mathbb{Z})\) transitive on primitives

Important

\(\{ \textit{primitives} \} = \mathbb{Q}\cup \infty \subset\) circle/projective line \(= \partial_\infty \mathbb{H}\)

Farey tessalation

\(\mathbb{Q}\cup \infty \subset\) circle/projective line

  • \((a,b)\text{ primitive } \mapsto a/b \in \mathbb{Q}\cup \infty\)
  • \(\begin{pmatrix} a & c \\ b & d \end{pmatrix} \in \mathrm{SL}(2,\mathbb{Z})\mapsto\) arc joining \((a/b, c/d)\)
  • \((a/b, c/d)\) are Farey neighbors

source

source

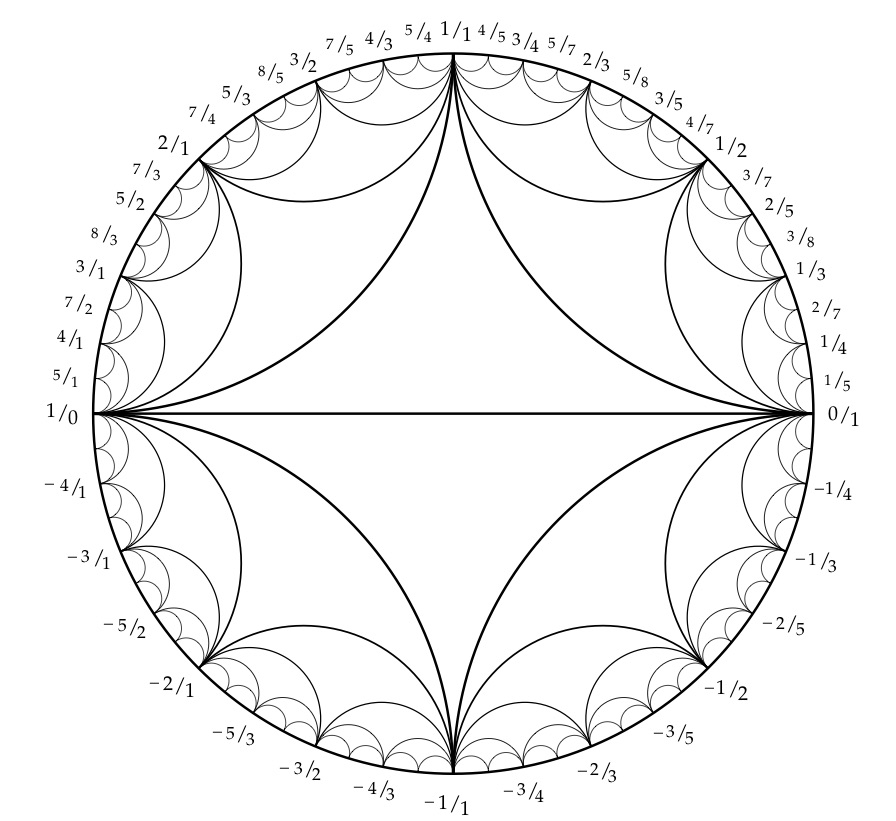
Definitions

  • arc = Poincaré geodesic joining \(a/b, c/d \in \mathbb{Q}\cup \infty\)
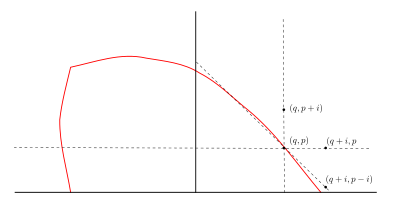
  • \(\lambda\)- length of arc \(= |ad - bc|^2\)

Lemma

\(\log \lambda\)- length = length of the portion outside Ford circles tangent to the real line at its endpoints

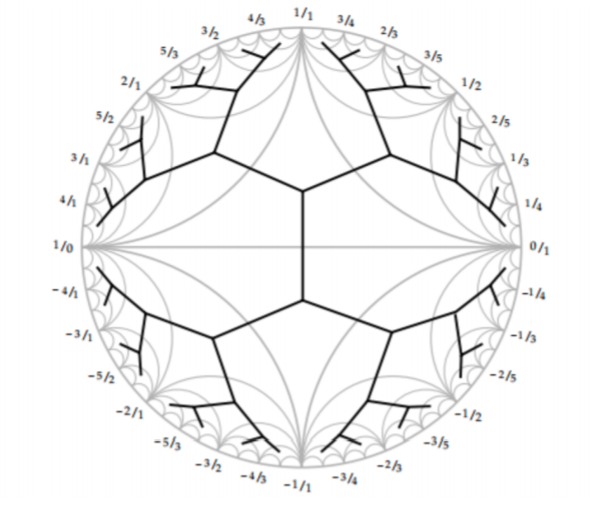
What is a Ford circle?

\(\mathrm{SL}(2,\mathbb{Z})\) acts by Mobius transformations on \(\mathbb{H}\)

  • \(\begin{pmatrix} a & c \\ b & d \end{pmatrix}.z = \frac{az+b}{cz+d}\)
  • preserves the Poincaré (hyperbolic) metric
  • the orbit of \(F := \{ z, \mathrm{Im}\, z > 1\}\) are the Ford circles

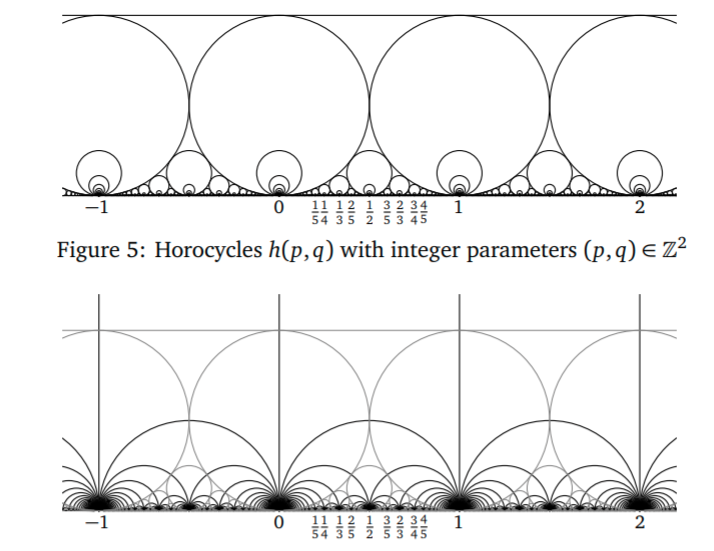
  • point of tangency with \(\mathbb{R} = p/q\), diameter = \(1/q^2\)

Lemma

  • arc joining \(a/b, c/d\) has \(\lambda\)- length \(= |ad - bc|^2\)
  • \(\log \lambda\)- length = length of the portion outside Ford circles tangent to the real line at its endpoints

remarks

  • the edges of the Farey tessalation have \(\lambda\) lengths 1
  • its diagonals have \(\lambda\) lengths 4

Proof of lemma

  • can suppose \(a/b = \infty\) and \(c/d = k/(ad - bc)\)
  • Ford circles \(F\) tangent at \(\infty\)
  • and another of diameter \(1/(ad - bc)^2\)

Important remark

the hyperbolic midpoint of this vertical arc is at height

\(\frac{1}{|ad - bc|}\)

quotients of \(\mathbb{H}^2\)

  • \(\Gamma = \mathrm{SL}(2,\mathbb{Z})\) has torsion so \(\mathbb{H}/\Gamma\) orbifold
  • \(\Gamma(2) = \ker (\mathrm{SL}(2,\mathbb{Z})\rightarrow \mathrm{SL}(2,\mathbb{F}_2))\)
  • \(\Gamma' = [\Gamma,\Gamma]\)
  • \(\mathbb{H}/\Gamma(2)\) three punctured sphere
  • \(\mathbb{H}/\Gamma'\) once punctured torus

A three punctured sphere
can be cut up into 2 ideal triangles.

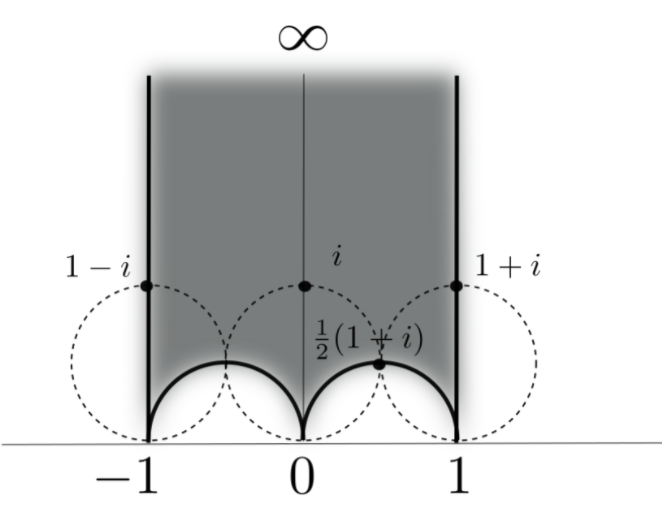
  • Fundamental domain for \(\Gamma(2)\)

  • \(i, 1+i, \frac12 ( 1 + i)\) are midpoints

reciprocals of sums of squares

  • \(i, 1+i, \frac12 ( 1 + i)\) are midpoints of arcs
  • the lifts to \(\mathbb{H}\) of the midpoints \(=\Gamma.i\)
  • \(\mathrm{Im} \frac{ai+b}{ci+d} = \frac{\mathrm{Im}\, i }{c^2 + d^2}= \frac{1}{c^2 + d^2}\)

\(\mathrm{Im} \frac{ai+b}{ci+d} = \frac{\mathrm{Im}\, i }{c^2 + d^2}= \frac{1}{c^2 + d^2}\)

What is the subgroup of automorphisms
fixing the cusp labeled \(\infty\)?

  • fixes the cusp and midpoint \(\frac12(1+i)\)
  • dashed geodesics are invariant under the group

subgroup lifts to

  • \(U': z \mapsto 2-\bar{z},\, V' : z \mapsto \bar{z}/(\bar{z} - 1)\)
  • composition is \(U'\circ V' : z \mapsto z \mapsto (-z + 2) /( z + 1)\)
  • whose fixed point is \(i+1\)

the set \(X\)

  • arcs joining cusps \(\infty, 1\) with \(\lambda\)-length \(p^2\)
  • lift to vertical lines with endpoints \(k/p\) with \(k\) odd
  • \(|X| = p - 1\) as before

Lemma A

  • Let \(n\) be a positive integer.
  • The number of ways of writing \(n\) as a sum of squares \(n = c^2 + d^2\) with \(c,d\) coprime integers
  • is equal to the number of integers \(0 \leq k < n-1\) coprime to \(n\) such that the line \(\{ k/n + i t,\, t>0 \}\) contains a point in the \(\Gamma\) orbit of \(i\).

action of generators

  • \(U': z \mapsto 2-\bar{z},\, V' : z \mapsto \bar{z}/(\bar{z} - 1)\)
  • composition is \(U'\circ V' : z \mapsto z \mapsto (-z + 2) /( z + 1)\)
  • whose fixed point is \(i+1\)

  • \(U': z \mapsto 2-\bar{z}\) induces an automorphism no fixed points in \(X,\, p \geq 3\)
  • \(V' : z \mapsto \bar{z}/(\bar{z} - 1)\) is an inversion in a circle with endpoints -1 and 1
  • projection to surface is simple arc of \(\lambda\)-length \(=4\)

Lemma B

The automorphism \(V\) induced by \(V'\)
fixes two and exactly two arcs in \(X\).

  • apply Burnside Lemma to prove Theorem 1.2
  • \(4 |X/G| = (p-1) + 2 + |X^{U\circ V}|\)

Proof

  • If \(\infty\) and \(k/p\) are exchanged by an inversion swapping Ford circles
  • Then the endpoints of the fixed circle are \((k-1)/p\) and \((k+1)/p\)
  • if \(1 < k < p-1\) the arc joining these points has \(\lambda\)-length = \(4p^2 >4\)

Button’s Theorem

If \(z\) is a Markoff number which is prime
then there is a unique triple \(z > y > x\)

  • Button’s theorem follows from unicity in \(z = c^2 + d^2\)
  • \(\Leftrightarrow\) unique vertical geodesic in Lemma A.
  • let’s look at that

  • The number of ways of writing \(n\) as a sum of squares \(n = c^2 + d^2\) with \(c,d\) coprime integers
  • is equal to the number of integers \(0 \leq k < n-1\) coprime to \(n\) such that the line \(\{ k/n + i t,\, t>0 \}\) contains a point in the \(\Gamma\) orbit of \(i\).
  • For every Markoff number \(m\) there are exactly 3 simple closed geodesics of length \(2\cosh^{-1}(3m/2)\) on the modular torus \(\mathbb{H}/\Gamma'\)
  • \(\Leftrightarrow\) exactly 3 simple arcs of \(\lambda\) length \(9m^2\) on \(\mathbb{H}/\Gamma'\)

The End