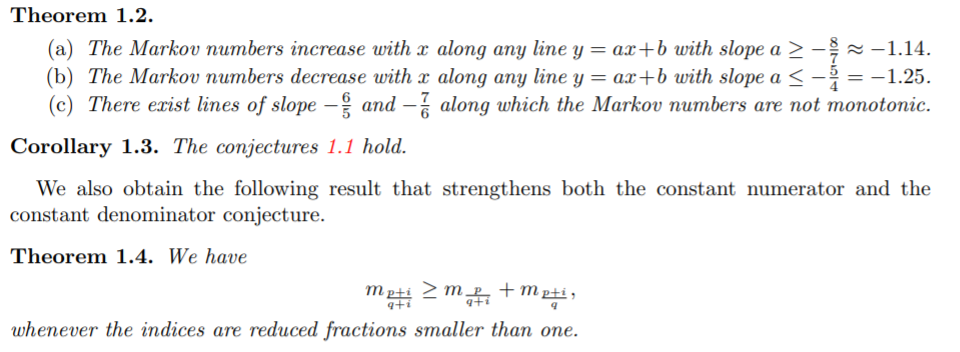Contents

• Character variety
• Norms and counting
• Proof of Aigner
• Proof by snakes (optional)
• Non convexity (optional

Character variety

H. Cohn, Approach to Markov’s Minimal Forms Through Modular Functions (1955)

• modular torus = quotient of upper half plane $\mathbb{H}$ by $\Gamma$ = commutator subgroup of $PSL(2,\mathbb{Z})$, acting by Mobius transformations
• relates Markoff numbers to lengths of simple closed geodesics

Back to the Torus

• $\mathbb{Z}^2$ acting on $\mathbb{R}^2$ by translation
• quotient space (orbit space) is a euclidean torus
• primitive elements $(p,q)\in \mathbb{Z}^2$
• $\rightarrow$ closed curve on torus = $(p,q)$ curve
• (usual) length $=\|(p,q)\| = \sqrt{p^2 + q^2}$

Usual Torus

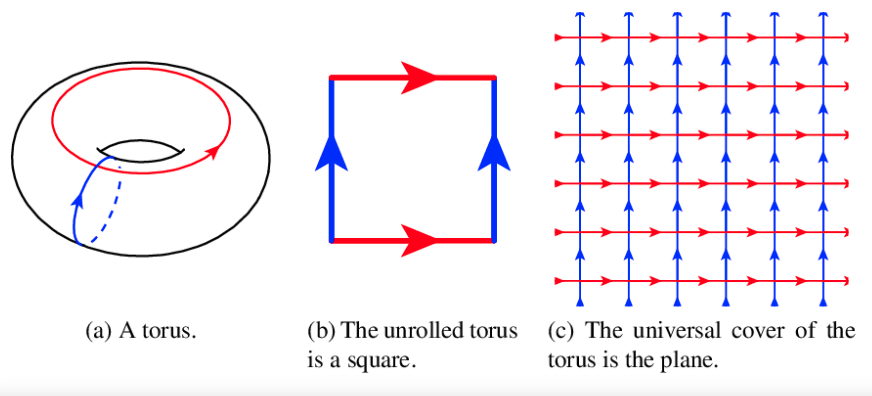
Torus

• $\mathbb{Z}^2$ acts by translation in lots of different ways
• translation lengths of $(1,0),(0,1),(1,-1)$ determine (up to conjugation)
• the representation $\mathbb{Z}^2 \rightarrow \text{isom}(\mathbb{R}^2)$
• length of $(p,q)$ curve given by quadratic form

representation $\mathbb{Z}^2 \rightarrow \text{isom}(\mathbb{R}^2)$

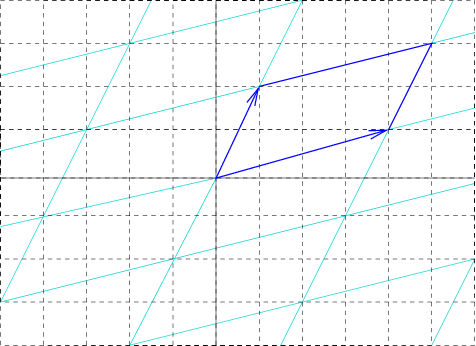
representation $\mathbb{Z}^2 \rightarrow \text{isom}(\mathbb{R}^2)$

Threes, triangles, tori

• 3 side lengths determine a triangle
• need 3 numbers to build a euclidean torus
• what about the 3 Markoff numbers ?
• can build a hyperbolic punctured torus
• no simple formula for length of $(p,q)$ curve

• modular torus = quotient of upper half plane $\mathbb{H}$ by $\Gamma$ = commutator subgroup of $\text{PSL}(2, \mathbb{Z})$, acting by Mobius transformations
• hyperbolic torus = quotient of upper half plane $\mathbb{H}$ by $\Gamma = \rho(\mathbb{Z}*\mathbb{Z})$,
• $\rho:\mathbb{Z}*\mathbb{Z}\rightarrow\text{PSL}(2, \mathbb{R})$ discrete faithful

Flat torus

Punctured torus

Geometry of the Markoff numbers

$\rho:\mathbb{Z}*\mathbb{Z}\rightarrow\text{PSL}(2, \mathbb{R})$

• lifts to $\hat{\rho}:\mathbb{Z}*\mathbb{Z}\rightarrow\text{SL}(2, \mathbb{R})$
• character map $\chi : \rho \mapsto ( tr \hat{\rho}(a), tr \hat{\rho}(b), tr \hat{\rho}(ab) )$
• $a,b$ generators of the free group = fundamental group of the torus.

Traces behave "like squares of translation lengths"

• parallogram law
• $b\in SL(2,\mathbb{C}),\,b^2 - (tr b)b + I_2 = 0$
• (Cayley-Hamilton) $\Rightarrow$
• $tr ab + tr ab^{-1} = (tr a) (tr b)$

Markoff cubic from the puncture

Loop round the puncture $aba^{-1}b^{-1}$

• isn't trivial but it's special (parabolic)
• corresponding matrix something like
• $\begin{pmatrix} \pm 1 & 6 \\ 0 & \pm 1 \end{pmatrix}$

puncture condition

$tr \hat{\rho} (aba^{-1}b^{-1}) = -2$

• $(x,y,z) = ( tr \hat{\rho}(a), tr \hat{\rho}(b), tr \hat{\rho}(ab) )$
• $x^2 + y^2 + z^2 - x y z = 2 + tr \hat{\rho} (aba^{-1}b^{-1})=0.$
• = Markoff cubic up to a change of variable

"inverse" character map

Section: character variety to representation variety

$\begin{pmatrix} x & -1 \\ 1 & 0 \end{pmatrix}$ $\begin{pmatrix} 0 & \eta \\ -\eta^{-1} & y \end{pmatrix}$

$z = \text{trace of product} = \eta + \eta^{-1}$

Cohn shows that the permutations and the Vieta flips used to construct Markov's binary tree are induced by automorphisms of the fundamental group of the torus.

Exo

• Nielsen move $(a,b,ab) \mapsto (a, b^{-1}, ab^{-1})$
• $tr ab + tr ab^{-1} = (tr a) (tr b)$

Counting problem

$N(t) =$ number of Markoff numbers $\leq t$

• $N(t) = C (\log(3t))^2 + O(\log t)$
• Zagier (1982) On the Number of Markov Numbers Below a Given Bound.
• Greg McShane, Igor Rivin A norm on homology of surfaces and counting simple geodesics

Counting closed simple geodesics

• character map $\chi : \rho \mapsto ( tr \hat{\rho}(a), tr \hat{\rho}(b), tr \hat{\rho}(ab) )$
• $a,b$ generators fundamental group of the torus.
• $a$ generator iff $\exists$ essential simple closed curves representing its conjugacy class

Simple representatives

Simple representatives in homology

$\phi : \mathbb{Z}*\mathbb{Z} \rightarrow \mathbb{Z}^2 \simeq H^1(T,\mathbb{Z})$ abelianizing homomorphism.

• generators $\in \mathbb{Z}*\mathbb{Z}$ $\mapsto$ primitive $\in \mathbb{Z}^2$.
• $(p,q) \in \mathbb{Z}^2$ primitive $\Leftrightarrow p,q$ coprime.

La norme

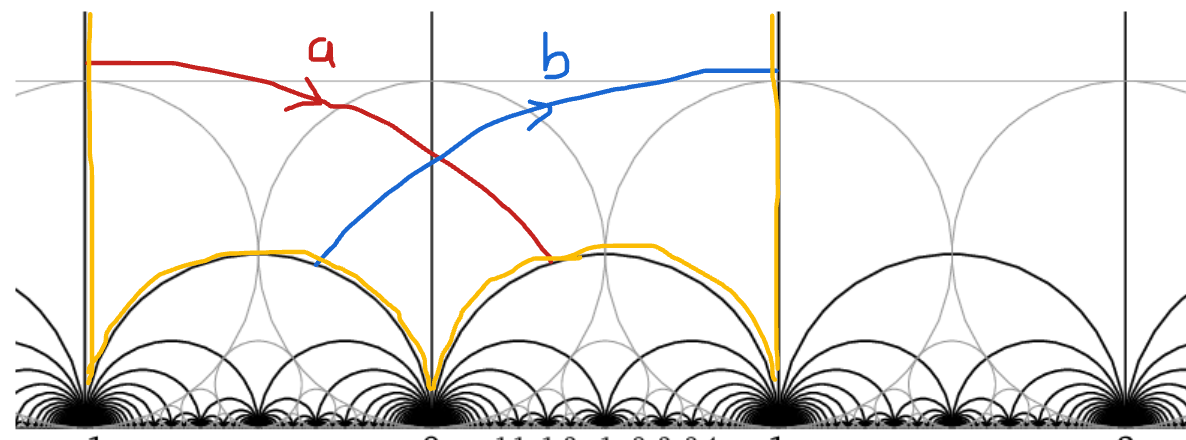
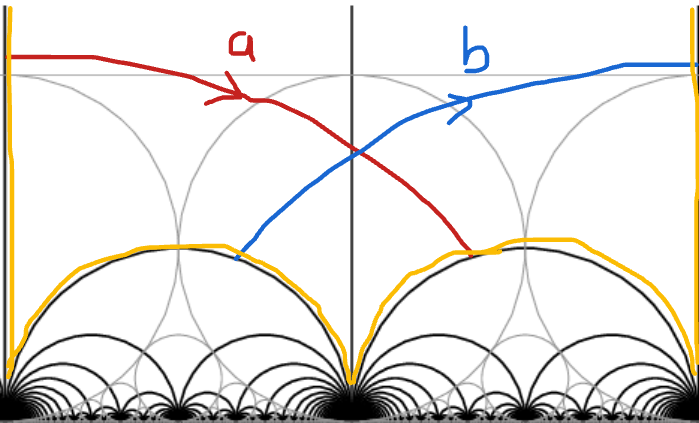
Let $c$ be an essential closed curve $\ell_c$ its length.

$\gamma \in H^1(T,\mathbb{Z}), \, \| \gamma \| := \inf_{ c \in \gamma} \ell_c/2$

• convexity/triangle inequality
• any pair of curves in linearly independent homology classes intersect
• a curve with self intersections is never a minimizer

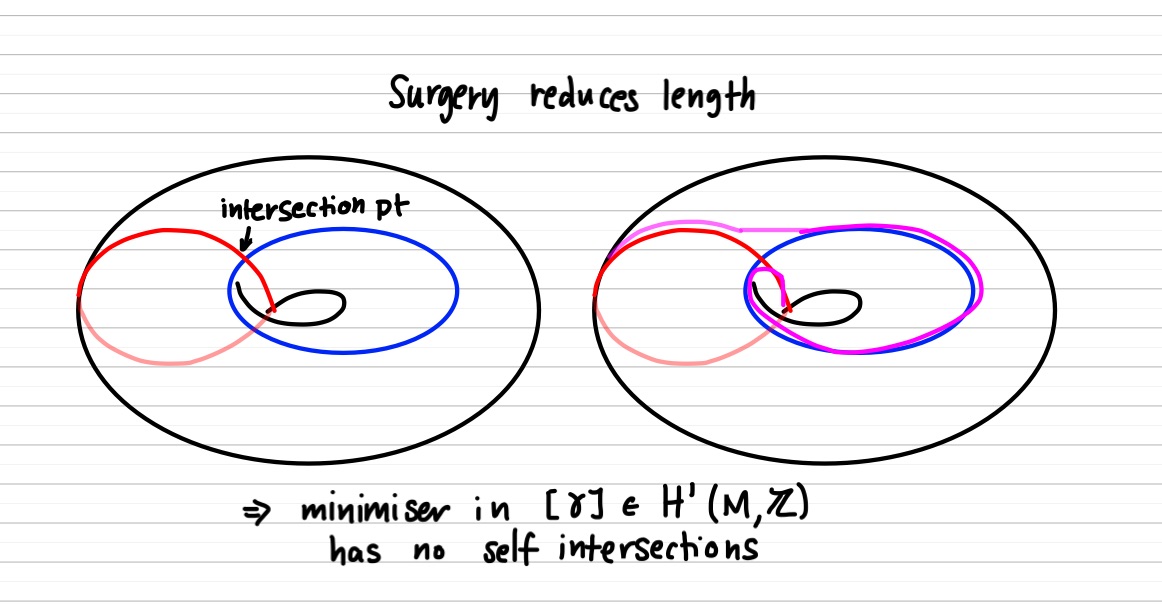
more formally from our paper

Unit ball

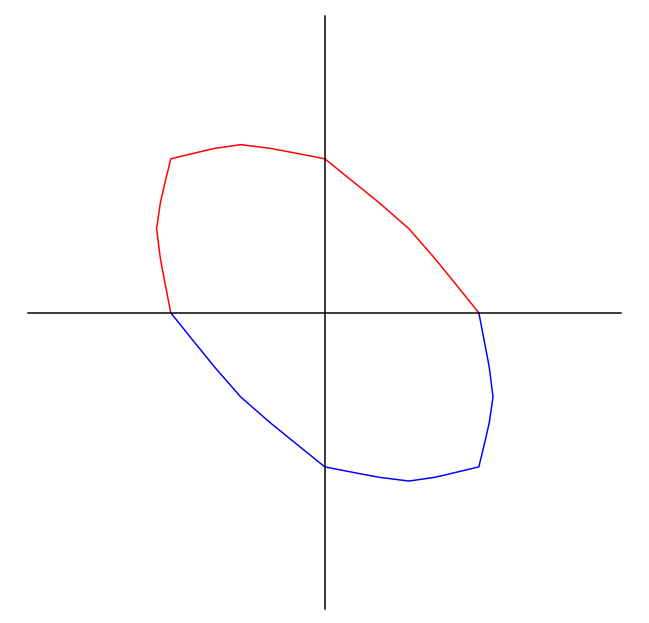
Corollary

The length function does not coincide with any reasonable function

• not differentiable at rational slopes
• is well approximated by piecewise linear

Unit ball and counting

• $\sharp \{ \gamma,\, \| \gamma \| \leq t \} \sim \text{area unit ball}\times t^2$
• $\sharp \{ \gamma \text{ primitive},\, \| \gamma \| \leq t \} \sim \frac{6}{\pi^2}\text{area unit ball}\times t^2$
• the area of the unit ball depends on the hyperbolic structure
• with Rivin we studied it, but now it's called the Mirzakhani function :(
• $\frac{6}{\pi^2}$ = proba 2 random integers coprime

Why log ?

$N(t) = C (\log 3 ))^2 + O(\log t)$

• $m_{p/q} = \frac13 tr \hat{\rho}( \gamma_{p/q})$
• $= \frac23 \cosh\left(\frac{\ell_{\gamma_p}}{2} \right)$
• $= \frac23 \cosh(\| (q,p) \|_s)$

Aigner's conjectures

Aigner's conjectures

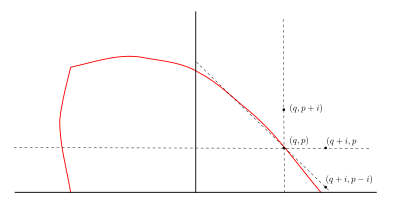
Let $p, q$ be real non negative numbers and $i > 0$ then

• $\|(q,p) \|_s < \|(q + i,p) \|_s$
• $\|(q,p) \|_s < \|(q ,p +i ) \|_s$
• If in addition $p < q$ then $\|(q ,p ) \|_s < \|(q + i ,p -i ) \|_s$

Aigners conjectures proof

source